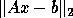Error Bounds for Linear Least Squares Problems

The linear least squares problem is to find x that minimizes 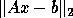. We discuss error bounds for the most common case where A is m-by-n with m > n, and A has full rank ; this is called an overdetermined least squares problem   (the following code fragments deal with m = n as well).

Let 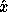be the solution computed by one of the driver routines xGELS, xGELSX or xGELSS (see section 2.2.2). An approximate error bound               

may be computed in one of the following ways, depending on which type of driver routine is used:

1. Suppose the simple driver SGELS is used:

      EPSMCH = SLAMCH( 'E' )
   *  Get the 2-norm of the right hand side B
      BNORM = SNRM2( M, B, 1 )
   *  Solve the least squares problem; the solution X
   *   overwrites B
      CALL SGELS( 'N', M, N, 1, A, LDA, B, LDB, WORK,
   $               LWORK, INFO )
      IF ( MIN(M,N) .GT. 0 ) THEN
   *     Get the 2-norm of the residual A*X-B
         RNORM = SNRM2( M-N, B( N+1 ), 1 )
   *     Get the reciprocal condition number RCOND of A
         CALL STRCON('I', 'U', 'N', N, A, LDA, RCOND,
   $                 WORK, IWORK, INFO)
         RCOND = MAX( RCOND, EPSMCH )
         IF ( BNORM .GT. 0.0 ) THEN
            SINT = RNORM / BNORM
         ELSE
            SINT = 0.0
         ENDIF
         COST = MAX( SQRT( (1.0E0 - SINT)*(1.0E0 + SINT) ),
   $                 EPSMCH )
         TANT = SINT / COST
         ERRBD = EPSMCH*( 2.0E0/(RCOND*COST) +
   $                      TANT / RCOND**2 )
      ENDIF
   

    

   For example, if ,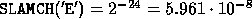

   

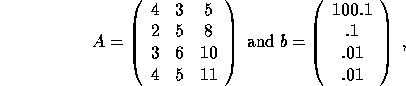
   then, to 4 decimal places,

   

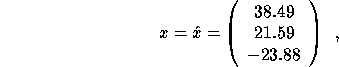
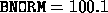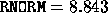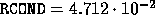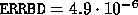   , , , , and the true error is .

2. Suppose the expert driver SGELSX is used.   This routine has an input argument RCND, which is used to determine the rank of the input matrix (briefly,   the matrix is considered not to have full rank if its condition number exceeds 1/RCND).   The code fragment below only computes error bounds if the matrix has been determined to have full rank. When the matrix does not have full rank, computing and interpreting error bounds is more complicated, and the reader is referred to the next section.

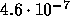      EPSMCH = SLAMCH( 'E' )
   *  Get the 2-norm of the right hand side B
      BNORM = SNRM2( M, B, 1 )
   *  Solve the least squares problem; the solution X
   *   overwrites B
      RCND = 0
      CALL SGELSX( M, N, 1, A, LDA, B, LDB, JPVT, RCND,
   $               RANK, WORK, INFO )
      IF ( RANK.LT.N ) THEN
         PRINT *,'Matrix less than full rank'
      ELSE IF ( MIN( M,N ) .GT. 0 ) THEN
   *     Get the 2-norm of the residual A*X-B
         RNORM = SNRM2( M-N, B( N+1 ), 1 )
   *     Get the reciprocal condition number RCOND of A
         CALL STRCON('I', 'U', 'N', N, A, LDA, RCOND,
   $                 WORK, IWORK, INFO)
         RCOND = MAX( RCOND, EPSMCH )
         IF ( BNORM .GT. 0.0 ) THEN
            SINT = RNORM / BNORM
         ELSE
            SINT = 0.0
         ENDIF
         COST = MAX( SQRT( (1.0E0 - SINT)*(1.0E0 + SINT) ),
   $                       EPSMCH )
         TANT = SINT / COST
         ERRBD = EPSMCH*( 2.0E0/(RCOND*COST) +
   $                      TANT / RCOND**2 )
      END IF
   

   The numerical results of this code fragment on the above A and b are the same as for the first code fragment.

3. Suppose the other type of expert driver SGELSS is used . This routine also has an input argument RCND, which is used to determine the rank of the matrix A. The same code fragment can be used to compute error bounds as for SGELSX, except that the call to SGELSX must be replaced by:

      CALL SGELSS( M, N, 1, A, LDA, B, LDB, S, RCND, RANK,
   $               WORK, LWORK, INFO )
   

   and the call to STRCON must be replaced by:

            RCOND = S( N ) / S( 1 )

    

   Applied to the same A and b as above, the computed 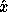is nearly the same, 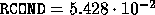, , 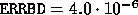and the true error is .

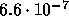• Further Details: Error Bounds for Linear Least Squares Problems