Next: ../STGIRONS/scalapack

Up: Presentation

Previous: ../SC94-LA/lapack-cray.tex

Speed in megaflops of Level 2 and Level 3 BLAS operations on a CRAY Y-MP

(all matrices are of order 500; U is upper triangular)

Level 1 BLAS [35]

: for vector operations, such as

Level 2 BLAS [18]

: for matrix-vector operations, such as

Level 3 BLAS [16]

: for matrix-matrix operations, such as

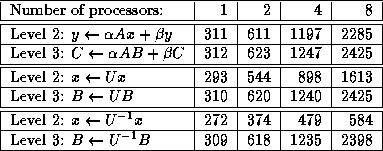
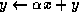
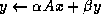
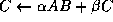
Here, A, B and C are matrices, x and y are vectors, and and 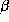are scalars.

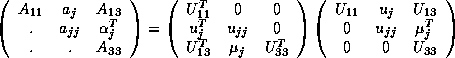
and equating coefficients of the 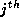column, we obtain:

Hence, if 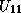has already been computed, we can compute 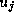and 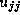from the equations:

Here is the body of the code of the LINPACK routine SPOFA, which implements the above method:

         DO 30 J = 1, N
            INFO = J
            S = 0.0E0
            JM1 = J - 1
            IF (JM1 .LT. 1) GO TO 20
            DO 10 K = 1, JM1
               T = A(K,J) - SDOT(K-1,A(1,K),1,A(1,J),1)
               T = T/A(K,K)
               A(K,J) = T
               S = S + T*T
   10       CONTINUE
   20       CONTINUE
            S = A(J,J) - S
C     ......EXIT
            IF (S .LE. 0.0E0) GO TO 40
            A(J,J) = SQRT(S)
   30    CONTINUE

    DO 10 J = 1, N
       CALL STRSV( 'Upper', 'Transpose', 'Non-unit', J-1, A, LDA,
   $               A(1,J), 1 )
       S = A(J,J) - SDOT( J-1, A(1,J), 1, A(1,J), 1 )
       IF( S.LE.ZERO ) GO TO 20
       A(J,J) = SQRT( S )
 10 CONTINUE

• change by itself is sufficient to make big gains in performance on a number of machines
  • from 72 to 251 megaflops for a matrix of order 500 on one processor of a CRAY Y-MP
    • 81% of the peak speed of matrix-matrix multiplication on this processor

• Virtually no difference in performance between the LINPACK-style and the LAPACK-style code.
  • about 23 megaflops

  • This is unsatisfactory on a machine on which matrix-matrix multiplication can run at 75 megaflops

• Re-cast as a block algorithm

To derive a block form of Cholesky factorization, we write the defining equation in partitioned form thus:

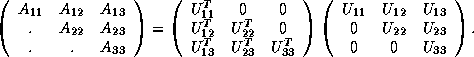
Equating submatrices in the second block of columns, we obtain:

Hence, if 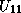has already been computed, we can compute 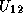as the solution to the equation

by a call to the Level 3 BLAS routine STRSM; and then we can compute 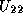from

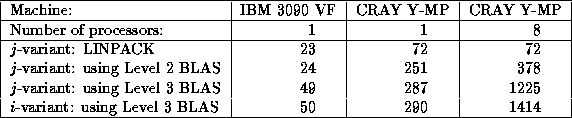
Speed in megaflops of Cholesky factorization 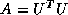for n = 500

   DO 10 J = 1, N, NB
      JB = MIN( NB, N-J+1 )
      CALL STRSM( 'Left', 'Upper', 'Transpose', 'Non-unit', J-1, JB,
  $               ONE, A, LDA, A(1,J), LDA )
      CALL SSYRK( 'Upper', 'Transpose', JB, J-1, -ONE, A(1,J), LDA,
  $               ONE, A(J,J), LDA )
      CALL SPOTF2( 'Upper', JB, A(J,J), LDA, INFO )
      IF( INFO.NE.0 ) GO TO 20
10 CONTINUE

This code runs at 49 megaflops on a 3090, more than double the speed of the LINPACK code. On a CRAY Y-MP, the use of Level 3 BLAS squeezes a little more performance out of one processor, but makes a large improvement when using all 8 processors.

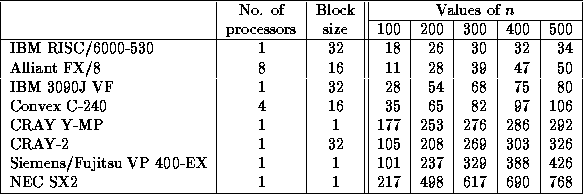
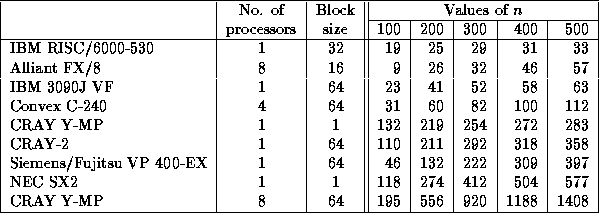
Speed in megaflops of SGETRF/DGETRF for square matrices of order n

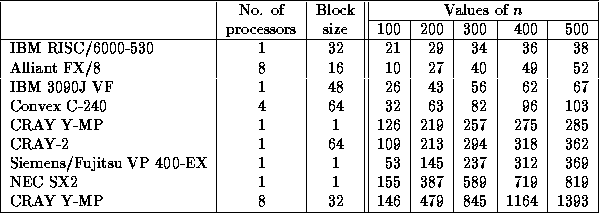
Speed in megaflops of SPOTRF/DPOTRF for matrices of order n with UPLO = `U'

Speed in megaflops of SSYTRF for matrices of order n with UPLO = `U' on a CRAY-2

• traditional algorithm for QR factorization is based on the use of elementary Householder-Householder transformation - blocked form matrices of the general form

  

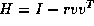
  where v is a column vector and r is a scalar. This leads to an algorithm with very good vector performance, especially if coded to use Level 2 BLAS.

• The key to developing a block form of this algorithm is to represent a product of b elementary Householder matrices of order n as a block form of a Householder matrix.

  

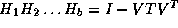
Speed in megaflops of SGEQRF/DGEQRF for square matrices of order n