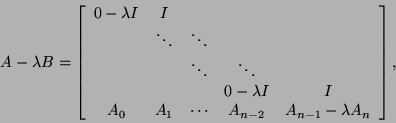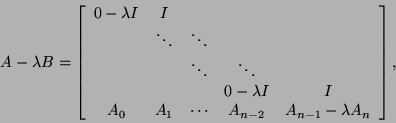Next: Example
Up: Generalized Non-Hermitian Eigenproblems
Previous: Specifying an Eigenproblem
Contents
Index
Related Eigenproblems
- If
 is nonsingular, then the NHEP
is nonsingular, then the NHEP
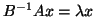 has the same eigenvalues
has the same eigenvalues 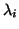 and
corresponding right eigenvectors
and
corresponding right eigenvectors 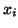 as
as
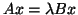 .
Similarly,
.
Similarly,
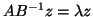 has the same eigenvalues
has the same eigenvalues 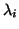 as
as
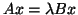 and right eigenvectors
and right eigenvectors
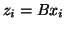 .
If
.
If  is nonsingular,
is nonsingular,
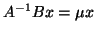 has the
same right eigenvectors
has the
same right eigenvectors 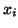 as
as
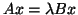 , and its eigenvalues are
reciprocals
, and its eigenvalues are
reciprocals
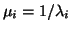 .
Finally, if
.
Finally, if  is nonsingular,
is nonsingular,
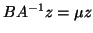 has reciprocal eigenvalues
has reciprocal eigenvalues
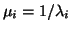 and right eigenvectors
and right eigenvectors 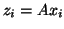 .
Analogous statements can be made about left eigenvectors.
.
Analogous statements can be made about left eigenvectors.
- More generally, suppose
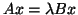 has eigenvalues
has eigenvalues 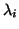 and corresponding right eigenvectors
and corresponding right eigenvectors 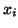 .
Let
.
Let 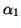 ,
, 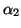 ,
, 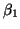 , and
, and 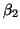 be scalars such that
be scalars such that
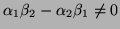 .
Then
.
Then
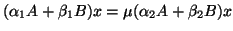 has the same eigenvectors
has the same eigenvectors 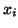 as
as
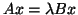 and
eigenvalues
and
eigenvalues
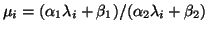 .
If one or both of
.
If one or both of
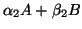 and
and
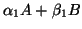 are nonsingular, then the method in item 1 above can be applied.
are nonsingular, then the method in item 1 above can be applied.
- Let
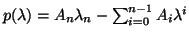 be
an
be
an  -by-
-by- matrix polynomial, where
matrix polynomial, where
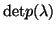 is not
identically zero.
An eigenpair
is not
identically zero.
An eigenpair
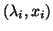 of
of 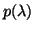 satisfies
satisfies
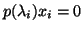 .
Define the
.
Define the 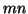 by
by 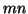 block companion pencil of
block companion pencil of 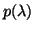 as
as
where all entries are  by
by  blocks and all entries not explicitly shown
are 0.
Then
blocks and all entries not explicitly shown
are 0.
Then
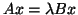 is a regular generalized eigenvalue problem,
and the eigenvalues of
is a regular generalized eigenvalue problem,
and the eigenvalues of 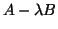 are the eigenvalues of
are the eigenvalues of 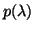 .
Note that there are
.
Note that there are 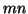 eigenvalues.
If
eigenvalues.
If
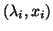 is an eigenpair of
is an eigenpair of 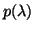 , then
, then
![$[ x_i^T, \lambda_i x_i^T , \ldots , \lambda_i^{n-1} x_i^T]^T$](img490.png) is a
right eigenvector of
is a
right eigenvector of  [194].
[194].





Next: Example
Up: Generalized Non-Hermitian Eigenproblems
Previous: Specifying an Eigenproblem
Contents
Index
Susan Blackford
2000-11-20