




Next: Example
Up: Non-Hermitian Eigenproblems J. Demmel
Previous: Specifying an Eigenproblem
Contents
Index
Related Eigenproblems
- Consider the GNHEP
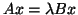 ,
where
,
where  and
and  are square and
are square and  is nonsingular. The
matrix
is nonsingular. The
matrix 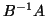 has the same eigenvalues and right eigenvectors as
has the same eigenvalues and right eigenvectors as
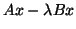 . If
. If 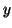 is a left eigenvector, i.e.,
is a left eigenvector, i.e.,
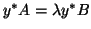 ,
,
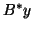 is a left eigenvector of
is a left eigenvector of 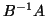 . Analogous statements are
true about
. Analogous statements are
true about 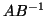 . If
. If 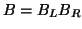 is a factorization of
is a factorization of  (from Gaussian elimination,
QR decomposition, or anything else),
(from Gaussian elimination,
QR decomposition, or anything else),
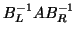 has the same
eigenvalues as
has the same
eigenvalues as  , right eigenvector
, right eigenvector 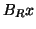 , and left eigenvector
, and left eigenvector 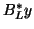 .
If
.
If  is well-conditioned, or
is well-conditioned, or 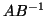 ,
, 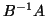 , or
, or
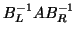 can be accurately computed, this is an effective way to solve
can be accurately computed, this is an effective way to solve
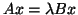 . If
. If  is ill-conditioned, it is preferable to
treat it as the GNHEP,
see §2.6.
is ill-conditioned, it is preferable to
treat it as the GNHEP,
see §2.6.
- Let
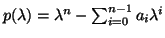 be a monic
polynomial. Define the
be a monic
polynomial. Define the  by
by  companion matrix of
companion matrix of 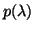 as
as
where all entries not explicitly shown are 0. Then the eigenvalues
of 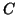 are the roots
are the roots 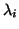 of
of
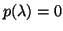 , and the right
eigenvectors
are
, and the right
eigenvectors
are
![$x_i = [ 1, \lambda_i , \ldots , \lambda_i^{n-1}]^T$](img481.png) .
.  is
not diagonalizable if
is
not diagonalizable if 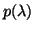 has multiple roots.
A reliable, but not optimally efficient, algorithm for finding roots
of a polynomial
has multiple roots.
A reliable, but not optimally efficient, algorithm for finding roots
of a polynomial 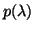 is to find all the eigenvalues of
is to find all the eigenvalues of 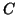 .
.
- Let
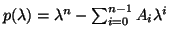 be a monic matrix polynomial,
where each
be a monic matrix polynomial,
where each 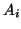 is an
is an  by
by  matrix.
An eigenpair
matrix.
An eigenpair
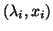 of
of 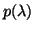 satisfies
satisfies
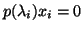 .
Define the
.
Define the 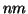 by
by 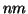 block companion matrix of
block companion matrix of 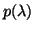 as
as
where all entries are  by
by  blocks and all entries not explicitly shown
are 0.
Then the eigenvalues
blocks and all entries not explicitly shown
are 0.
Then the eigenvalues 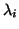 of
of 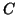 are the eigenvalues of
are the eigenvalues of 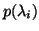 .
Note that there are
.
Note that there are 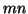 eigenvalues.
If
eigenvalues.
If
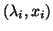 is an eigenpair of
is an eigenpair of 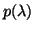 , then
, then
![$[ x_i^T, \lambda_i x_i^T , \ldots , \lambda_i^{n-1} x_i^T]^T$](img490.png) is a
right eigenvector of
is a
right eigenvector of 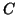 [194].
[194].





Next: Example
Up: Non-Hermitian Eigenproblems J. Demmel
Previous: Specifying an Eigenproblem
Contents
Index
Susan Blackford
2000-11-20



