




Next: General Framework of Preconditioning
Up: Preconditioned Eigensolvers A. Knyazev
Previous: Preconditioned Eigensolvers A. Knyazev
Contents
Index
Introduction
We consider a generalized symmetric definite
eigenvalue problem of the form
with real symmetric  by
by  matrices
matrices  and
and  , assuming that
, assuming that
 is positive definite.
That describes a regular matrix pencil
is positive definite.
That describes a regular matrix pencil
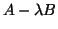 with a discrete spectrum, a set of
with a discrete spectrum, a set of
 real, some possibly infinite, eigenvalues
real, some possibly infinite, eigenvalues
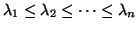 . If
. If
 is nonsingular, all eigenvalues are finite.
If
is nonsingular, all eigenvalues are finite.
If  is positive semidefinite (e.g.,
is positive semidefinite (e.g., 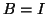 ), all eigenvalues are
positive,
and we consider the problem of computing
the smallest
), all eigenvalues are
positive,
and we consider the problem of computing
the smallest  eigenvalues of the pencil
eigenvalues of the pencil 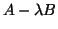 .
When
.
When  is indefinite, it is convenient to consider
the pencil
is indefinite, it is convenient to consider
the pencil 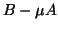 with eigenvalues
with eigenvalues
where we want to compute
the largest  eigenvalues,
eigenvalues,
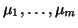 .
The problem of computing
.
The problem of computing  smallest eigenvalues
smallest eigenvalues 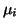 can be reformulated as the previous one by replacing
can be reformulated as the previous one by replacing
 with
with 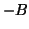 . In buckling, both largest and smallest
eigenvalues
. In buckling, both largest and smallest
eigenvalues 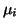 are of interest.
are of interest.
It is well known that (right) eigenvectors 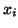 ,
satisfying
,
satisfying
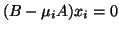 ,
can be chosen orthogonal in the following sense:
,
can be chosen orthogonal in the following sense:
An important class of eigenproblems
is the class of mesh eigenproblems,
arising from discretizations of boundary value problems
with self-adjoint differential operators of mathematical physics.
The following properties are typical for mesh eigenproblems:
- The size
 of
of  and
and  is big, and is
much larger than the number
is big, and is
much larger than the number  of required eigenpairs.
Sometimes, a family of similar eigenproblems with increasing
of required eigenpairs.
Sometimes, a family of similar eigenproblems with increasing
 must be solved.
must be solved.
 and
and  are sparse. Very large
matrices cannot always fit in available memory even when using a sparse
representation. In some situations,
matrices
are sparse. Very large
matrices cannot always fit in available memory even when using a sparse
representation. In some situations,
matrices  and
and  are not available in an explicit matrix form.
are not available in an explicit matrix form.
- No cheap factorization of
 ,
or any matrix of the form
,
or any matrix of the form 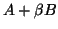 , is available.
The only operation we can perform with
, is available.
The only operation we can perform with  is multiplication
of a vector by
is multiplication
of a vector by  .
.
- Cheap factorization of
 may sometimes be available, but,
in general, the only operation we can do efficiently with
may sometimes be available, but,
in general, the only operation we can do efficiently with  is multiplication of a vector by
is multiplication of a vector by  .
.
- The matrix
 is ill-conditioned.
Usually,
is ill-conditioned.
Usually,  has a smaller condition number than
has a smaller condition number than  .
.
- The number of wanted eigenpairs
 can be chosen
such that eigenvalues of interest
are well separated from the rest of the spectrum; in other words,
the ratio
can be chosen
such that eigenvalues of interest
are well separated from the rest of the spectrum; in other words,
the ratio
is not too small. This means that the invariant subspace
of the matrix 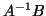 spanned by the eigenvectors of interest is well conditioned,
thus the problem of computing
spanned by the eigenvectors of interest is well conditioned,
thus the problem of computing  eigenpairs is well posed.
Such property can be established in many applications when
the spectrum of the pencil
eigenpairs is well posed.
Such property can be established in many applications when
the spectrum of the pencil 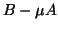 approximates
a spectrum of a compact operator, such that
zero is the only point of condensation of the approximate eigenvalues.
approximates
a spectrum of a compact operator, such that
zero is the only point of condensation of the approximate eigenvalues.
Such problems appear, e.g., in structural mechanics, where
it is usual to call  a stiffness
matrix and
a stiffness
matrix and  a mass matrix. A mass matrix is usually
positive definite, but in some applications, e.g., in buckling, the
matrix
a mass matrix. A mass matrix is usually
positive definite, but in some applications, e.g., in buckling, the
matrix
 is only nonnegative, or even indefinite, while
is only nonnegative, or even indefinite, while  is positive
definite.
is positive
definite.
In the rest of the section, for brevity we deal with the pencil
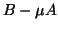 only. With
only. With 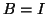 and
and
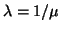 ,
our results and arguments are readily applied for the pencil
,
our results and arguments are readily applied for the pencil
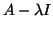 .
.
Now, we briefly consider two traditional
methods for such generalized eigenproblems.
One popular approach is based on multiplication by
a shift-and-invert operator:
see §4.3.
It lets us quickly compute the eigenvalues
closest to the shift 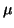 , assuming that
this operation may be implemented with an explicit efficient triangular
factorization
of
, assuming that
this operation may be implemented with an explicit efficient triangular
factorization
of 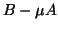 .
With a properly chosen variable shift,
e.g., based on the Rayleigh quotient
(x) = (x,Bx)(x,Ax),
the convergence is cubic for symmetric eigenproblems.
However, for very large problems such factorizations are
usually too expensive. Instead of explicit factorization,
an approximate solution of the corresponding linear system
is possible, e.g., using an iterative system solver. Then we obtain
an inner-outer iterative method, where outer iterations may
slow down significantly for an insufficient number of inner steps.
If we take into account the total number of
inner-outer iterative steps, the convergence is usually only
linear.
.
With a properly chosen variable shift,
e.g., based on the Rayleigh quotient
(x) = (x,Bx)(x,Ax),
the convergence is cubic for symmetric eigenproblems.
However, for very large problems such factorizations are
usually too expensive. Instead of explicit factorization,
an approximate solution of the corresponding linear system
is possible, e.g., using an iterative system solver. Then we obtain
an inner-outer iterative method, where outer iterations may
slow down significantly for an insufficient number of inner steps.
If we take into account the total number of
inner-outer iterative steps, the convergence is usually only
linear.
If a preconditioned iterative solver is used for inner iterations,
such a method becomes a preconditioned eigensolver. We shall discuss
this method later, in §11.3.7.
Another approach can be used if  is efficiently factorizable,
so that we can multiply vectors by
is efficiently factorizable,
so that we can multiply vectors by 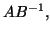 or
or 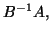 and use traditional methods like the Lanczos method;
see §4.4.
In this case, a single iteration is not too expensive,
but the convergence may be slow.
If
and use traditional methods like the Lanczos method;
see §4.4.
In this case, a single iteration is not too expensive,
but the convergence may be slow.
If  is indefinite, then we need to find eigenvalues
is indefinite, then we need to find eigenvalues 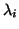 in the middle of the spectrum using polynomial methods,
which is known to be a hard problem.
If
in the middle of the spectrum using polynomial methods,
which is known to be a hard problem.
If  is positive definite, then the situation is simpler, as
we want to find the extreme (smallest) eigenvalues
is positive definite, then the situation is simpler, as
we want to find the extreme (smallest) eigenvalues 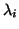 .
Still, the ratio
.
Still, the ratio
that typically characterizes the speed of convergence for 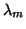 is small because of the large denominator,
which is a sign of possibly slow convergence.
is small because of the large denominator,
which is a sign of possibly slow convergence.
Thus, the traditional approaches considered above are usually
inefficient
for very large eigenproblems. Preconditioning is a key
for significant improvement of the performance.





Next: General Framework of Preconditioning
Up: Preconditioned Eigensolvers A. Knyazev
Previous: Preconditioned Eigensolvers A. Knyazev
Contents
Index
Susan Blackford
2000-11-20
![]() ,
satisfying
,
satisfying
![]() ,
can be chosen orthogonal in the following sense:
,
can be chosen orthogonal in the following sense:
![]() a stiffness
matrix and
a stiffness
matrix and ![]() a mass matrix. A mass matrix is usually
positive definite, but in some applications, e.g., in buckling, the
matrix
a mass matrix. A mass matrix is usually
positive definite, but in some applications, e.g., in buckling, the
matrix
![]() is only nonnegative, or even indefinite, while
is only nonnegative, or even indefinite, while ![]() is positive
definite.
is positive
definite.
![]() only. With
only. With ![]() and
and
![]() ,
our results and arguments are readily applied for the pencil
,
our results and arguments are readily applied for the pencil
![]() .
.
![]() is efficiently factorizable,
so that we can multiply vectors by
is efficiently factorizable,
so that we can multiply vectors by ![]() or
or ![]() and use traditional methods like the Lanczos method;
see §4.4.
In this case, a single iteration is not too expensive,
but the convergence may be slow.
If
and use traditional methods like the Lanczos method;
see §4.4.
In this case, a single iteration is not too expensive,
but the convergence may be slow.
If ![]() is indefinite, then we need to find eigenvalues
is indefinite, then we need to find eigenvalues ![]() in the middle of the spectrum using polynomial methods,
which is known to be a hard problem.
If
in the middle of the spectrum using polynomial methods,
which is known to be a hard problem.
If ![]() is positive definite, then the situation is simpler, as
we want to find the extreme (smallest) eigenvalues
is positive definite, then the situation is simpler, as
we want to find the extreme (smallest) eigenvalues ![]() .
Still, the ratio
.
Still, the ratio