




Next: Preconditioned Eigensolvers A. Knyazev
Up: Inexact Methods K. Meerbergen
Previous: Example 11.2.3.
Contents
Index
Inexact Shift-and-Invert
Recall from §11.2.1 that with exact arithmetic and
exact linear system solvers, the SI and the
Cayley
transform produce the same Krylov spaces and the same Ritz pairs.
We have shown in the previous sections by theoretical arguments and
numerical
examples that the Cayley transform is a good choice when the linear
systems
are solved with a relative error tolerance 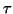 smaller than 1.
smaller than 1.
When the Cayley transform is used, the linear system
is solved, where
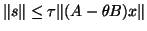 .
This linear system can be written as
.
This linear system can be written as
So, with
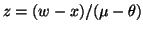 and
and
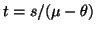 , we
obtain the
shift-and-invert linear system
, we
obtain the
shift-and-invert linear system
where
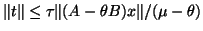 .
In other words, we can use the SI, but instead of
a relative residual tolerance, we should use a tolerance that is proportional
to the norm of the Ritz residual,
.
In other words, we can use the SI, but instead of
a relative residual tolerance, we should use a tolerance that is proportional
to the norm of the Ritz residual,
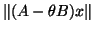 .
.
Susan Blackford
2000-11-20