




Next: Solvers.
Up: Parallelism J. Dongarra and
Previous: Vector Updates.
Contents
Index
Matrix-Vector Products.
The matrix-vector products are often easily parallelized on shared memory
machines by splitting the matrix in strips of rows corresponding to the vector
segments. Each processor then computes the matrix-vector product of one
strip.
For distributed memory machines, there may be a problem if each processor
has only a segment of the vector in its memory. Depending on the bandwidth
of the matrix, we may need communication for other elements of the vector,
which may lead to communication bottlenecks. However, many sparse
matrix problems arise from a network in which only nearby nodes are
connected. For example, matrices stemming
from finite difference or finite element problems typically involve
only local connections: matrix element 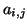 is nonzero
only if variables
is nonzero
only if variables 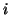 and
and 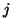 are physically close.
In such a case, it seems natural to subdivide the network, or
grid, into suitable blocks and to distribute them over the processors.
When computing
are physically close.
In such a case, it seems natural to subdivide the network, or
grid, into suitable blocks and to distribute them over the processors.
When computing 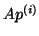 , each processor requires the values of
, each processor requires the values of 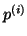 at
some nodes in neighboring blocks. If the number of connections to these
neighboring blocks is small compared to the number of internal nodes,
then the communication time can be overlapped with computational work.
at
some nodes in neighboring blocks. If the number of connections to these
neighboring blocks is small compared to the number of internal nodes,
then the communication time can be overlapped with computational work.
More recently, graph partitioning has been used as a powerful tool
to deal with the general problems with nonlocal connections.
Consider
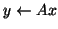 and the undirected graph
and the undirected graph 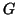 of the (symmetric)
matrix
of the (symmetric)
matrix  . Assume vertex
. Assume vertex 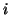 stores
stores 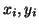 , and the nonzero
, and the nonzero 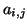 for
all
for
all 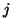 . Let vertex
. Let vertex 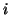 represent the job of computing
represent the job of computing
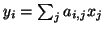 . We can assign weight of vertex
. We can assign weight of vertex 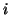 to be
the number of operations for computing
to be
the number of operations for computing 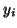 , and the weight of
edge
, and the weight of
edge 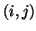 to be 1, which represents the cost of sending
to be 1, which represents the cost of sending 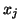 to
vertex
to
vertex 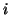 if vertices
if vertices 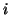 and
and 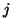 were mapped on different processors.
A good graph partitioning heuristic would partition
were mapped on different processors.
A good graph partitioning heuristic would partition 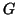 into
into 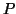 subsets
of vertices corresponding to
subsets
of vertices corresponding to 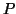 processors, such that:
processors, such that:
- the sums of vertex weights are approximately equal among the subsets,
- the sum of edge cuts crossing the subsets is minimized.
This ensures a good load balance and minimizes communication.
Good graph partitioning software includes Chaco [223]
and METIS [259] (also ParMETIS, the parallel version).
After partitioning, further optimizations can be performed to reduce
communication. For example, if a subset of vertices contains
several edges to another subset, the corresponding elements of the
vector can be packed into one message, so that each processor sends no
more than one message to another processor.
For more detailed discussions on implementation aspects for distributed
memory systems, see De Sturler and van der Vorst [111,112] and
Pommerell [369].
High-quality parallel algorithms for distributed memory machines are
implemented in software packages such as Aztec [236]
and PETSc [38].
The software can be obtained via the book's homepage, ETHOME.





Next: Solvers.
Up: Parallelism J. Dongarra and
Previous: Vector Updates.
Contents
Index
Susan Blackford
2000-11-20
![]() and the undirected graph
and the undirected graph ![]() of the (symmetric)
matrix
of the (symmetric)
matrix ![]() . Assume vertex
. Assume vertex ![]() stores
stores ![]() , and the nonzero
, and the nonzero ![]() for
all
for
all ![]() . Let vertex
. Let vertex ![]() represent the job of computing
represent the job of computing
![]() . We can assign weight of vertex
. We can assign weight of vertex ![]() to be
the number of operations for computing
to be
the number of operations for computing ![]() , and the weight of
edge
, and the weight of
edge ![]() to be 1, which represents the cost of sending
to be 1, which represents the cost of sending ![]() to
vertex
to
vertex ![]() if vertices
if vertices ![]() and
and ![]() were mapped on different processors.
A good graph partitioning heuristic would partition
were mapped on different processors.
A good graph partitioning heuristic would partition ![]() into
into ![]() subsets
of vertices corresponding to
subsets
of vertices corresponding to ![]() processors, such that:
processors, such that: