CDS Matrix-Vector Product

If the $n \times n$ matrix $A$ is stored in CDS format, it is still possible to perform a matrix-vector product $y=Ax$ by either rows or columns, but this does not take advantage of the CDS format. The idea is to make a change in coordinates in the doubly nested loop. Replacing $j\rightarrow i+j$ we get

$$y_i\leftarrow y_i+a_{i,j}x_j \quad\Rightarrow\quad y_i\leftarrow y_i+a_{i,i+j}x_{i+j} ~.$$

With the index $i$ in the inner loop we see that the expression $a_{i,i+j}$ accesses the $j$th diagonal of the matrix (where the main diagonal has number 0).

The algorithm will now have a doubly nested loop with the outer loop enumerating the diagonals diag=-p,q with $p$ and $q$ the (nonnegative) numbers of diagonals to the left and right of the main diagonal. The bounds for the inner loop follow from the requirement that

$$1\leq {\tt i},{\tt i+j}\leq n. \pagebreak$$

The algorithm becomes

   for i = 1, n
       y(i) = 0
   end;
   for diag = -diag_left, diag_right
       for loc = max(1,1-diag), min(n,n-diag)
           y(loc) = y(loc) + val(loc,diag) * x(loc+diag)
       end;
   end;

The transpose matrix-vector product $y=A^Tx$ is a minor variation of the algorithm above. Using the update formula

$$\begin{eqnarray*} y_i&\leftarrow&y_i+a_{i+j,i}x_j \\ &=&y_i+a_{i+j,i+j-j}x_{i+j} \end{eqnarray*}$$

we obtain

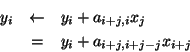
   for i = 1, n
       y(i) = 0
   end;
   for diag = -diag_right, diag_left
       for loc = max(1,1-diag), min(n,n-diag)
           y(loc) = y(loc) + val(loc+diag, -diag) * x(loc+diag)
       end;
   end;

The memory access for the CDS-based matrix-vector product $y=Ax$ (or $y=A^Tx$) is three vectors per inner iteration. On the other hand, there is no indirect addressing, and the algorithm is vectorizable with vector lengths of essentially the matrix order $n$. Because of the regular data access, most machines can perform this algorithm efficiently by keeping three base registers and using simple offset addressing.