




Next: Geometric Technicalities
Up: Modifying the Templates
Previous: Under the Hood
Contents
Index
Here is a sketch of specific modifications a user
may wish to make on the code.
- Line minimization.
Currently, line minimizations are being performed by
the MATLAB functions
fmin and fzero
through the wrappers Fline, dFline, and
gradline. However, one may have better ways
to line-minimize within an optimization
routine or one may wish to supplement fmin
and fzero for reasons of economy.
- High-level algorithms. The user may wish to use a
minimization routine differing from or more sophisticated than
the methods currently available, or one may have a different
stopping criterion [17] that we did not anticipate. It is
possible to adapt other flat optimization algorithms to
new
sg_ algorithms
without having to know too many details.
Most unconstrained minimizations
contain line searches (y 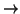
y+t*v),
Hessian applications
(H*v), and inner products (v'w). To properly geometrize the
algorithm, one has to do no more than replace these components with
move(Y,V,t), dgrad(Y,V), and ip(Y,V,W), respectively.
- Hessian inversion. We currently provide codes to invert the
covariant Hessian in the functions
invdgrad_CG (which uses a conjugate
gradient method) and invdgrad_MINRES (which uses a MINRES
algorithm).
Any matrix inversion routine which can stably
invert black box linear operators could be used in place of these, and
no other modifications to the code would be required.
- Workspaces. To make the code more readable we have not
implemented any workspace variables even though there are many
computations which could be reused. For example, in the objective
function group, for many of the sample problems, products of the form
A*Y or Y*B or complicated matrix functions of Y
such as B(Y) in the Jordan example could be saved in a
workspace. Some of the terms in the computation of grad and
dgrad could likewise be saved (in fact, our current
implementation essentially recomputes the gradient every time the
covariant Hessian is applied).
- In-lining. Although we have separated the
tangent
and dtangent functions from the grad and dgrad
functions, one often finds that when these functions are in-lined,
some terms cancel out and therefore do not need to be computed.
One might also consider in-lining the move function when
performing line minimizations so that one could reuse data to make
function evaluations and point updates faster.
- Sphere or
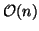 geometry. Some problems are always set
on the unit sphere or on
geometry. Some problems are always set
on the unit sphere or on 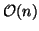 , both of which have simpler geometries
than the Stiefel manifold. Geodesics on both are easier to compute,
as are tangent projections. To take advantage of this, one should
modify the geometric implementation group.
, both of which have simpler geometries
than the Stiefel manifold. Geodesics on both are easier to compute,
as are tangent projections. To take advantage of this, one should
modify the geometric implementation group.
- Globals. In order to have adaptable and readable code, we
chose to use global structures,
SGParameters and
FParameters, to hold data which could be put in the
argument lists of all the functions. The user may wish to modify
his/her code so that this data is passed explicitly to each function
as individual arguments.
- Preconditioning. The Hessian solve by conjugate
gradient routine,
invdgrad, does not have any preconditioning
step. Conjugate gradient can perform very poorly without preconditioning,
and the preconditioning of black box linear operators like dgrad
is a very difficult problem. The user might try to find a
good preconditioner for dgrad.





Next: Geometric Technicalities
Up: Modifying the Templates
Previous: Under the Hood
Contents
Index
Susan Blackford
2000-11-20