




Next: Error Bound for Computed
Up: Stability and Accuracy Assessments
Previous: Transfer Residual Errors to
Contents
Index
Error Bound for Computed Eigenvalues.
From (7.105) and the
perturbation theory of eigenvalues and eigenvectors, it can shown that
up to the first order of
residual norms 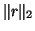 and
and
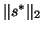 ,
there is an eigenvalue
,
there is an eigenvalue  of
of  satisfying
satisfying
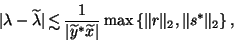 |
(212) |
where ``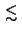 '' denotes ``less than'' up to the first order of
'' denotes ``less than'' up to the first order of
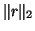 and
and
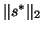 .
Note that
the individual condition number
.
Note that
the individual condition number 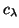 is defined as
is defined as
and 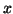 and
and 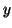 are the corresponding eigenvector and left
eigenvector of
are the corresponding eigenvector and left
eigenvector of  and are normalized so that
and are normalized so that
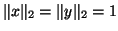 .
Since exact
.
Since exact 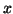 and
and 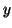 usually are not known, for
all practical purposes, one could simply estimate this condition number
usually are not known, for
all practical purposes, one could simply estimate this condition number
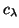 by
by
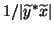 instead.
Notice that
instead.
Notice that
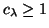 , with equality if
, with equality if  is Hermitian.
is Hermitian.
If the approximate left eigenvector 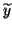 is not available, bounds
directly on
is not available, bounds
directly on
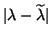 do not exist in general.
The equation (7.104) would be the only thing available
to explain the accuracy of the
computed eigenvalues
do not exist in general.
The equation (7.104) would be the only thing available
to explain the accuracy of the
computed eigenvalues 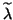 and
and 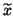 .
.





Next: Error Bound for Computed
Up: Stability and Accuracy Assessments
Previous: Transfer Residual Errors to
Contents
Index
Susan Blackford
2000-11-20
![]() is not available, bounds
directly on
is not available, bounds
directly on
![]() do not exist in general.
The equation (7.104) would be the only thing available
to explain the accuracy of the
computed eigenvalues
do not exist in general.
The equation (7.104) would be the only thing available
to explain the accuracy of the
computed eigenvalues ![]() and
and ![]() .
.