




Next: Purging .
Up: Orthogonal Deflating Transformation
Previous: Locking or Purging a
Contents
Index
The first instance to discuss is the locking of a single converged
Ritz value. Assume that
with
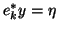 , where
, where
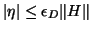 .
Here, it is understood that
.
Here, it is understood that
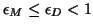 is a specified
relative accuracy tolerance between
is a specified
relative accuracy tolerance between 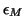 and
and 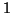 .
.
If 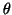 is ``wanted" then it is desirable to lock
is ``wanted" then it is desirable to lock 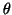 .
However, in order to accomplish this it will be necessary to
arrange a transformation of the current Arnoldi factorization
to one with a small subdiagonal to isolate
.
However, in order to accomplish this it will be necessary to
arrange a transformation of the current Arnoldi factorization
to one with a small subdiagonal to isolate 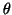 .
This may be accomplished by constructing a
.
This may be accomplished by constructing a 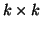 orthogonal
matrix
orthogonal
matrix 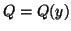 using Algorithm 7.8:
using Algorithm 7.8:
with
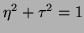 .
.
Now, when we apply
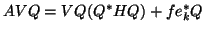 , we obtain
, we obtain
Unfortunately, 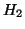 is not upper Hessenberg. Further work will have to
be done to bring it to Hessenberg form. This must be done without disturbing
the form of the residual term
is not upper Hessenberg. Further work will have to
be done to bring it to Hessenberg form. This must be done without disturbing
the form of the residual term
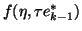 . We need to
construct an orthogonal
. We need to
construct an orthogonal  such that
such that
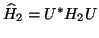 is
upper Hessenberg and
is
upper Hessenberg and
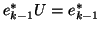 . This can be done with
Householder transformations or with a variant of the transformations
defined in Algorithm 7.8
working from the last row upwards. The following MATLAB
code segment shows a slightly inefficient way to obtain such a
. This can be done with
Householder transformations or with a variant of the transformations
defined in Algorithm 7.8
working from the last row upwards. The following MATLAB
code segment shows a slightly inefficient way to obtain such a 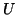 .
.
rev = [k-1:-1:1];
C = H_2';
[U,H_2] = hess(C(rev,rev));
U = U(rev,rev);
H_2 = H_2(rev,rev)';
Once 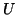 is constructed, replace
is constructed, replace 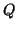 with
with
![$Q : Q [{1 \atop 0}\;{0 \atop U}]$](img2050.png) , and
the end result of these transformations will be
Av_1 &=& v_1 + f , where
v_1^* f = 0,
, and
the end result of these transformations will be
Av_1 &=& v_1 + f , where
v_1^* f = 0,
A V_2 &=& [v_1, V_2] [ c h^*,
H_2
] + f e_k-1^* ,
where
![$[v_1 , V_2] = V Q$](img1056.png) and
and 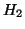 is upper Hessenberg.
After this, all subsequent implicit restarting takes place as if
is upper Hessenberg.
After this, all subsequent implicit restarting takes place as if
All the subsequent orthogonal transformations
associated with implicit restarting are applied to 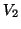 and
and
![$[{h^* \atop H_2}] $](img2053.png) while never disturbing the relation
while never disturbing the relation
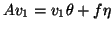 .
In subsequent Arnoldi steps,
.
In subsequent Arnoldi steps, 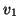 participates in the orthogonalization
so that the selective orthogonalization recommended by Parlett and
Scott [363,353] is accomplished automatically.
participates in the orthogonalization
so that the selective orthogonalization recommended by Parlett and
Scott [363,353] is accomplished automatically.





Next: Purging .
Up: Orthogonal Deflating Transformation
Previous: Locking or Purging a
Contents
Index
Susan Blackford
2000-11-20
![]() is ``wanted" then it is desirable to lock
is ``wanted" then it is desirable to lock ![]() .
However, in order to accomplish this it will be necessary to
arrange a transformation of the current Arnoldi factorization
to one with a small subdiagonal to isolate
.
However, in order to accomplish this it will be necessary to
arrange a transformation of the current Arnoldi factorization
to one with a small subdiagonal to isolate ![]() .
This may be accomplished by constructing a
.
This may be accomplished by constructing a ![]() orthogonal
matrix
orthogonal
matrix ![]() using Algorithm 7.8:
using Algorithm 7.8:
![]() , we obtain
, we obtain