




Next: Transfer Residual Error to
Up: Positive Definite
Previous: Positive Definite
Contents
Index
Residual Vector.
Let 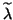 be a computed eigenvalue, and let
be a computed eigenvalue, and let
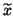 be its corresponding computed eigenvector.
For the simplicity of the presentation,
we normalize the computed eigenvector so that
be its corresponding computed eigenvector.
For the simplicity of the presentation,
we normalize the computed eigenvector so that
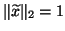 .
The corresponding residual vector or
residual error is defined by
.
The corresponding residual vector or
residual error is defined by
Ideally, we would like to have 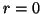 , but in practice
, but in practice 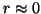 .
It is conceivable that a small residual error implies
good accuracy in the computed
.
It is conceivable that a small residual error implies
good accuracy in the computed 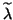 and
and 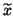 .
We are interested in knowing how accurate the computed
.
We are interested in knowing how accurate the computed
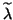 and
and 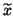 are, given
are, given 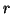 .
.
Susan Blackford
2000-11-20