Convergence Properties

There is a fairly straightforward intuitive explanation of how this repeated updating of the starting vector $v_1$ through implicit restart might lead to convergence. If $v_1$ is expressed as a linear combination of eigenvectors $\{x_j\}$ of $A$, then

$$v_1 = \sum_{j=1}^n x_j \gamma_j \quad \Rightarrow \quad \psi(A)v_1 = \sum_{j=1}^n x_j \psi(\lambda_j) \gamma_j .$$

Applying the same polynomial (i.e., using the same shifts) repeatedly for $\ell$ iterations will result in the $j$th original expansion coefficient being attenuated by a factor

$$\left( \frac{\psi(\lambda_j)}{\psi(\lambda_1)} \right)^{\ell} \ ,$$

where the eigenvalues have been ordered according to decreasing values of $\vert\psi(\lambda_j)\vert$. The leading $k$ eigenvalues become dominant in this expansion and the remaining eigenvalues become less and less significant as the iteration proceeds. Hence, the starting vector $v_1$ is forced into an invariant subspace as desired. The adaptive choice provided with the exact shift mechanism further enhances the isolation of the wanted components in this expansion, and the wanted eigenvalues are approximated better and better as the iteration proceeds.

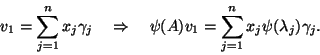
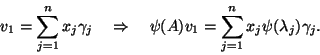
It is worth noting that if $m = n$, then $r_{m} = 0$ and this iteration is precisely the same as the implicitly shifted QR iteration. Even for $m<n$, the first $k$ columns of $V_m$ and the leading $k \times k$ tridiagonal submatrix of $T_m$ are mathematically equivalent to the matrices that would appear in the full implicitly shifted QR iteration using the same shifts $\mu_j.$ In this sense, the IRLM may be viewed as a truncation of the implicitly shifted QR iteration. The fundamental difference is that the standard implicitly shifted QR iteration selects shifts to drive subdiagonal elements of $T_n$ to zero from the bottom up while the shift selection in the implicitly restarted Lanczos method is made to drive subdiagonal elements of $T_m$ to zero from the top down. Of course, convergence of the implicit restart scheme here is like a ``shifted power" method, while the full implicitly shifted QR iteration is like an ``inverse iteration" method.

Thus the exact shift strategy can be viewed both as a means to damp unwanted components from the starting vector and also as directly forcing the starting vector to be a linear combination of wanted eigenvectors. See [419] for information on the convergence of IRLM and [22,421] for other possible shift strategies for Hermitian $A.$ The reader is referred to [293,334] for studies comparing implicit restart with other schemes.