




Next: Acceleration.
Up: Subspace Iteration
Previous: Subspace Dimension.
Contents
Index
Locking.
Because of the different rates of convergence of each of the
approximate eigenvalues computed by the subspace iteration, it is
common practice to extract them one at a time and perform a type of
deflation. Thus, as soon as the first eigenvector has converged there
is no need to continue to multiply it by  in the subsequent
iterations. Indeed, we can freeze this vector and work only with the
vectors
in the subsequent
iterations. Indeed, we can freeze this vector and work only with the
vectors
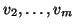 . However, we will still need to perform
the subsequent orthogonalizations with respect to the frozen vector
. However, we will still need to perform
the subsequent orthogonalizations with respect to the frozen vector
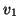 whenever such orthogonalizations are needed. The term used for
this strategy is locking;
that is, we do not further attempt to improve the locked approximation
for
whenever such orthogonalizations are needed. The term used for
this strategy is locking;
that is, we do not further attempt to improve the locked approximation
for 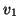 .
.
The following algorithm describes a practical subspace iteration with
deflation (locking) for computing the 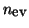 dominant eigenvalues.
dominant eigenvalues.

We now describe some implementation details.
- (1)
- The initial starting matrix
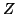 should be constructed
to be dominant in eigenvector directions of interest in order to
accelerate convergence. When no such information is known
a priori, a random matrix is as good a choice as any
other.
should be constructed
to be dominant in eigenvector directions of interest in order to
accelerate convergence. When no such information is known
a priori, a random matrix is as good a choice as any
other.
- (4)
- The iteration parameter
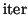 should be chosen to
minimize orthonormalization cost while maintaining a
reasonable amount of numerical accuracy. The amplification factor
should be chosen to
minimize orthonormalization cost while maintaining a
reasonable amount of numerical accuracy. The amplification factor
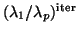 , where the eigenvalues
, where the eigenvalues 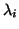 are ordered in decreasing absolute values, gives the loss of accuracy. Rutishauser [381] plays it safe and allows an amplification factor of only
are ordered in decreasing absolute values, gives the loss of accuracy. Rutishauser [381] plays it safe and allows an amplification factor of only 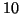 , losing one decimal, while Stewart and Jennings [426] let
the algorithm run to
, losing one decimal, while Stewart and Jennings [426] let
the algorithm run to 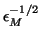 , half the machine accuracy, but not to more than 10 iterations.
, half the machine accuracy, but not to more than 10 iterations.





Next: Acceleration.
Up: Subspace Iteration
Previous: Subspace Dimension.
Contents
Index
Susan Blackford
2000-11-20
![]() dominant eigenvalues.
dominant eigenvalues.