


Next: Determining the total execution
Up: Allowing for communication-computation overlap
Previous: Allowing for communication-computation overlap
Hypotheses (H2), (H3) and (H4) may appear very restricting. However,
we point out the following justifications:
- Tile shape
- We assume that the tiles are rectangular. This is to be understood as the outcome of previous program transformations.
The first step in tiling amounts to determining the best
size and size of the tiles, assuming an infinite grid of virtual processors.
Because this step will lead to tiles whose edges are parallel to extremal dependence vectors in the convex hull
of the dependence cone, we can perform a unimodular transformation and rewrite the original loop nest along the edge axes. The resulting domain may not be a rectangular, but we can approximate it using the smallest bounding box.
- Dependence vectors
- We assume that dependences are summarized by the vector pair
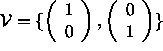 . Note that these
are dependences between tiles, not between elementary computations. In Example 1, we had 5 dependence vectors in the original loop nest,
but we ended up with
. Note that these
are dependences between tiles, not between elementary computations. In Example 1, we had 5 dependence vectors in the original loop nest,
but we ended up with 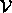 after tiling. This is a very general situation if the tiles are large enough. For instance,
having a dependence vector
(0,a) with
after tiling. This is a very general situation if the tiles are large enough. For instance,
having a dependence vector
(0,a) with 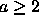 between tiles, instead of having vector (0,1),
would mean unusually long dependences in the loop nest (in Example 1,
a(i,j) would depend upon a(i,j-8) but not on a(i,j-x) for
between tiles, instead of having vector (0,1),
would mean unusually long dependences in the loop nest (in Example 1,
a(i,j) would depend upon a(i,j-8) but not on a(i,j-x) for 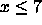 ).
Note that having (0,a) in addition to (0,1) as a dependence
vector between tiles is simply redundant.
).
Note that having (0,a) in addition to (0,1) as a dependence
vector between tiles is simply redundant.
On the other hand, hypotheses (H5) and (H6) are unnecessarily restrictive,
because the mapping and scheduling of the tiles should be an output decision of the procedure of tiling with limited resources, rather than being given a priori. We overcome this restriction in Section 3.5.
Jack Dongarra
Sat Feb 8 08:17:58 EST 1997
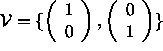 . Note that these
are dependences between tiles, not between elementary computations. In Example 1, we had 5 dependence vectors in the original loop nest,
but we ended up with
. Note that these
are dependences between tiles, not between elementary computations. In Example 1, we had 5 dependence vectors in the original loop nest,
but we ended up with 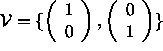 . Note that these
are dependences between tiles, not between elementary computations. In Example 1, we had 5 dependence vectors in the original loop nest,
but we ended up with
. Note that these
are dependences between tiles, not between elementary computations. In Example 1, we had 5 dependence vectors in the original loop nest,
but we ended up with