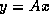CRS Matrix-Vector Product

The matrix vector product 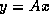using CRS format can be expressed in the usual way:

since this traverses the rows of the matrix . For an 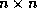matrix A, the matrix-vector multiplication is given by

for i = 1, n 
    y(i)  = 0 
    for j = row_ptr(i), row_ptr(i+1) - 1
        y(i) = y(i) + val(j) * x(col_ind(j))
    end;
end;

Since this method only multiplies nonzero matrix entries, the operation count is 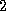times the number of nonzero elements in , which is a significant savings over the dense operation requirement of .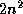

For the transpose product 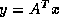we cannot use the equation

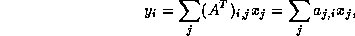
since this implies traversing columns of the matrix, an extremely inefficient operation for matrices stored in CRS format. Hence, we switch indices to

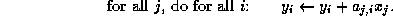
The matrix-vector multiplication involving 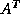is then given by

for i = 1, n
    y(i) =  0
end;
for j = 1, n
    for i = row_ptr(j), row_ptr(j+1)-1
        y(col_ind(i)) = y(col_ind(i)) + val(i) * x(j)
    end;
end;

Both matrix-vector products above have largely the same structure, and both use indirect addressing. Hence, their vectorizability properties are the same on any given computer. However, the first product (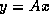) has a more favorable memory access pattern in that (per iteration of the outer loop) it reads two vectors of data (a row of matrix and the input vector ) and writes one scalar. The transpose product (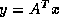) on the other hand reads one element of the input vector, one row of matrix , and both reads and writes the result vector . 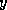Unless the machine on which these methods are implemented has three separate memory paths (e.g., Cray Y-MP), the memory traffic will then limit the performance. This is an important consideration for RISC-based architectures.