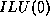 and
and  -
-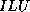 factorizations coincide, and,
as remarked above, we only have to calculate the pivots of the
factorization; other elements in the triangular factors are equal to
off-diagonal elements of
factorizations coincide, and,
as remarked above, we only have to calculate the pivots of the
factorization; other elements in the triangular factors are equal to
off-diagonal elements of  .
.
We will now consider the special case of
a matrix derived from central differences on a Cartesian product grid.
In this case the 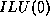 and
and  -
-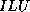 factorizations coincide, and,
as remarked above, we only have to calculate the pivots of the
factorization; other elements in the triangular factors are equal to
off-diagonal elements of
factorizations coincide, and,
as remarked above, we only have to calculate the pivots of the
factorization; other elements in the triangular factors are equal to
off-diagonal elements of  .
.
In the following we will assume a natural, line-by-line, ordering of the grid points.
Letting 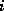 ,
,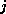 be coordinates in a regular 2D grid, it is easy to see
that the pivot on grid point
be coordinates in a regular 2D grid, it is easy to see
that the pivot on grid point 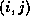 is only determined by
pivots on points
is only determined by
pivots on points 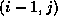 and
and 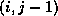 . If there are
. If there are  points on
each of
points on
each of  grid lines,
we get the following generating relations for the pivots:
grid lines,
we get the following generating relations for the pivots:
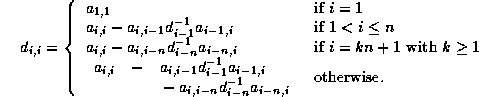
Conversely, we can describe the factorization algorithmically as
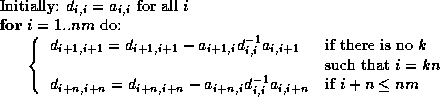
In the above we have assumed that the variables in the problem are ordered according to the so-called ``natural ordering'': a sequential numbering of the grid lines and the points within each grid line. Below we will encounter different orderings of the variables.