Summary and Conclusions

  In this paper we have described a parallel left-looking algorithm for performing the out-of-core LU factorization of dense matrices. Use of out-of-core storage adds an extra layer to the hierarchical memory. In order to manage flexible and efficient access to this extra layer of memory an extra level of partitioning over matrix columns has been introduced into the standard ScaLAPACK algorithm. This is represented by the superblocks in the hybrid algorithm that we have described. The hybrid algorithm is left-looking at the outermost loop level, but uses a right-looking algorithm to factor the individual superblocks. This permits the trade-offs between I/O cost, communication cost, and load imbalance overhead to be controlled at the application level by varying the parameters of the data distribution and the superblock width.

We have implemented the out-of-core LU factorization algorithm on an Intel Paragon parallel computer. The implementation makes use of a small library of parallel I/O routines called the BLAPIOS, together with ScaLAPACK and PBLAS routines. From a preliminary performance study we have observed the following.

1. On the Paragon the version of the algorithm that stores the matrix in pivoted form is faster than the version that stores matrices in unpivoted form.
2. On the Paragon the parallel I/O system cannot efficiently and reliably manage large numbers of open files if the volume of data being read is sufficiently large. We have therefore implemented logically distributed files using a single file partitioned among the processes.
3. We have a broad qualitative understanding of the performance. Increasing the superblock width by increasing should decrease I/O costs, but this was found to be true only up to a point on the Paragon because when the volume of parallel I/O becomes too great, I/O performance starts to degrade. Thus, although it might be expected that the optimal approach would be a make the superblock as large as possible, this will not be fastest on all systems.

Future work will follow two main directions. We will seek to implement our out-of-core algorithm on other platforms, such as the IBM SP-2, symmetric multiprocessors, and clusters of workstations. The use of the MPI-IO library will be considered as a means of providing portability for our code, rather than implementing the BLAPIOS directly on each machine. We will also develop a more sophisticated analytical performance model, and use it to interpret our timings. The IBM SP-2 will be of particular interest as each processor is attached to its own disk. Hence, unlike our Paragon implementation, it may prove appropriate on the IBM SP-2 to implement logically distributed matrices as physically distributed matrices.

As network bandwidths continue to improve, networks of workstations may prove to be a good environment for research groups needing to perform very large LU factorizations. Such a system is cost-effective compared with supercomputers such as the Intel Paragon, and is under the immediate control of the researchers using it. Moreover, disk storage is cheap and easy to install. Consider the system requirements if we want to factor a matrix in 24 hours. In a balanced system we might expect to spend 8 hours computing, 8 hours communicating over the network, and 8 hours doing I/O. Such a computation would require about floating-point operations, or 23 Gflop/s. If there are workstations and each has 128 Mbytes of memory, then the maximum superblock width is elements. The I/O per workstation is then,

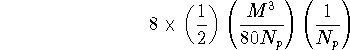
or Gbyte per workstation. The total amount of data communicated between processes can be approximated by the communication volume of the matrix multiplication operations that asymptotically dominate. The total amount of communication is approximately elements, where is the superblock width. Assuming again that the superblock width is , the total amount of communication is approximately elements. So for 16 workstations, each would need to compute at about 1.5 Gflop/s, and perform I/O at about 6.8 Mbyte/s. A network bandwidth of about 145 Mbyte/s would be required. Each workstation would require 5 Gbyte of disk storage. These requirements are close to the capabilities of current workstation networks.