LINPACK



Next: LAPACK
Up: Dense Linear Algebra
Previous: EISPACK
LINPACK
is a collection of Fortran subroutines that analyze
and solve linear equations and linear least-squares problems.
The package solves linear systems whose matrices are
general, banded, symmetric indefinite,
symmetric positive definite, triangular, and tridiagonal square.
In addition, the package computes the QR and
singular value decompositions of rectangular matrices and
applies them to least-squares problems.
LINPACK is organized around four matrix factorizations: LU
factorization, Cholesky factorization, QR factorization,
and singular value decomposition. The term LU factorization is used here
in a very general sense to mean the factorization of a square matrix into
a lower triangular part and an upper triangular part, perhaps with
pivoting.
LINPACK uses column-oriented algorithms to
increase efficiency by
preserving locality of reference.
By column orientation we mean that the LINPACK codes always reference arrays
down columns, not across rows. This works because Fortran stores arrays in
column major
order. Thus, as one proceeds down a column of an array, the memory references
proceed sequentially in memory. On the other hand, as one proceeds across a
row,
the memory references jump across memory, the length of the jump being
proportional to the length of a column.
The effects of column orientation
are quite dramatic: on systems with virtual or cache memories, the LINPACK
codes will significantly outperform codes that are not column oriented.
We note, however, that
textbook examples of matrix algorithms are seldom column oriented.
Another important factor influencing the efficiency of LINPACK is the use of
the Level 1 BLAS; there are three effects.
First, the overhead entailed in calling
the BLAS reduces the efficiency of the code. This reduction is negligible
for large matrices, but it can be quite significant for small matrices. The
matrix size at which it becomes unimportant varies from system to system; for
square matrices it is typically between 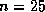 and
and 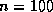 . If this
seems like an unacceptably large overhead, remember that on many
modern systems the solution of a system of order 25 or less is itself
a negligible calculation. Nonetheless, it cannot be denied that a person
whose programs depend critically on solving small matrix problems in inner
loops will be better off with BLAS-less versions of the LINPACK codes.
Fortunately, the BLAS can be removed from the smaller, more frequently used
program in a short editing session.
. If this
seems like an unacceptably large overhead, remember that on many
modern systems the solution of a system of order 25 or less is itself
a negligible calculation. Nonetheless, it cannot be denied that a person
whose programs depend critically on solving small matrix problems in inner
loops will be better off with BLAS-less versions of the LINPACK codes.
Fortunately, the BLAS can be removed from the smaller, more frequently used
program in a short editing session.
Second, the BLAS improve the efficiency of programs when they are run on
nonoptimizing
compilers. This is because doubly subscripted array references in the inner
loop
of the algorithm are replaced by singly subscripted array references in the
appropriate BLAS. The effect can be seen for matrices of quite small order,
and for large orders the savings are quite significant.
Finally, improved efficiency can be achieved by coding a set of BLAS
[18]
to take advantage of the special features of the computers on which LINPACK is
being
run. For most computers, this simply means producing machine-language
versions.
However, the code can also take advantage of more exotic architectural
features, such as vector operations.
Further details about the BLAS are presented in Section 2.3.



Next: LAPACK
Up: Dense Linear Algebra
Previous: EISPACK
Jack Dongarra
Wed Jun 21 02:35:11 EDT 1995
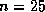 and
and 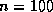 . If this
seems like an unacceptably large overhead, remember that on many
modern systems the solution of a system of order 25 or less is itself
a negligible calculation. Nonetheless, it cannot be denied that a person
whose programs depend critically on solving small matrix problems in inner
loops will be better off with BLAS-less versions of the LINPACK codes.
Fortunately, the BLAS can be removed from the smaller, more frequently used
program in a short editing session.
. If this
seems like an unacceptably large overhead, remember that on many
modern systems the solution of a system of order 25 or less is itself
a negligible calculation. Nonetheless, it cannot be denied that a person
whose programs depend critically on solving small matrix problems in inner
loops will be better off with BLAS-less versions of the LINPACK codes.
Fortunately, the BLAS can be removed from the smaller, more frequently used
program in a short editing session.