 Problem Representation
Problem Representation
 Problem Representation
Problem RepresentationFirst we discuss the type of individual matrix or operator entries. The simplest distinction is between real and complex data. The issues are speed (real arithmetic is faster than complex), storage (real numbers require half the storage of complex numbers), code complexity (some algorithms simplify greatly if we can do complex arithmetic), and stability (real arithmetic can guarantee complex conjugate eigenvalues of real matrices). The distinction between single and double precision, which clearly affects space, will be discussed again as an accuracy issue.
Given the type of individual operator entries, we must distinguish the overall structure of the operator. Here is our list. Two letter abbreviations (like GE) refer to matrix types supported by LAPACK [Table 2.1]lapackmanual2.
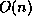 data.
data.
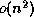 data.
It turns out that the relevant classification is by the operations that can
be performed on the operators represented, not the details of the
representation. This will be clearer in
Section 4.5.
data.
It turns out that the relevant classification is by the operations that can
be performed on the operators represented, not the details of the
representation. This will be clearer in
Section 4.5.
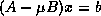
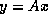 (and
(and 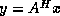 )
(this includes, for
example, ``dense'' integral operators which have fast algorithms
for performing
)
(this includes, for
example, ``dense'' integral operators which have fast algorithms
for performing 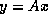 .)
.)
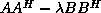 or
or
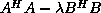 ,
or
,
or 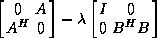 , perhaps shifted
, perhaps shifted
There are many more special structures, often arising from control theory, such as unitary orthogonal matrices represented by their Schur parameters. Until we hear of a large demand for such problems, we do not plan to include them, other than as literature references. For the same reason we also do not plan to include algorithms for quaternion matrices, or matrices with rational entries, which are more properly included in the domain of symbolic computation.