What we plan not to include



Next: Desired Spectral Information
Up: Mathematical Properties
Previous: What we plan
Some of them we may include, provided there is sufficient demand.
Mostly, we would limit ourselves to literature references.
- There is a variety of ``non-linear'' eigenproblems which can
be linearized in various ways and converted to the above problems
- Rational problems
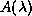
- General nonlinear problems
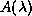
- Polynomial system zero finding
- The SVD can be used to solve a variety of least squares problems, and
these may best be solved by representing the SVD in ``factored'' form.
These factored SVD algorithms are somewhat complicated and hard to
motivate without the least squares application, but there are a great
many least squares problems, but including too many of them (beyond
references to the literature) would greatly expand the scope of this project.
The same comments apply to the generalized SVD, of which there are even more
variations.
- Eigenproblems from systems and control.
There is a large source of eigenproblems, many of which can
be reduced to finding certain kinds of spectral information about
possibly singular pencils
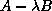 . These problems arise with
many kinds of special structures, many of which have been exploited in
special packages, some of them can be solved by general algorithms.
For example, solutions of Riccati equations are often
reduced to eigenproblems.
A comprehensive treatment of these problems would greatly expand the
scope of the book, but including some treatment seems important.
. These problems arise with
many kinds of special structures, many of which have been exploited in
special packages, some of them can be solved by general algorithms.
For example, solutions of Riccati equations are often
reduced to eigenproblems.
A comprehensive treatment of these problems would greatly expand the
scope of the book, but including some treatment seems important.
- Structured singular value problems,
also called
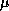 -analysis by its practitioners
These
problems must generally be solved by optimization techniques, and indeed
NP-completeness results exist for some of them. We believe that the
algorithms in our proposed book would be called within inner loops
for these optimization algorithms, and we should simply refer to the
literature for this application. The same comment applies for other
optimization problems based on eigenvalues (e.g. finding the nearest
unstable matrix).
-analysis by its practitioners
These
problems must generally be solved by optimization techniques, and indeed
NP-completeness results exist for some of them. We believe that the
algorithms in our proposed book would be called within inner loops
for these optimization algorithms, and we should simply refer to the
literature for this application. The same comment applies for other
optimization problems based on eigenvalues (e.g. finding the nearest
unstable matrix).
- Generalized singular value decompositions of more than two matrices
- Computing matrix functions like
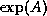 or
or 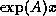 , or
for multivariate
eigenvalue problems
, or
for multivariate
eigenvalue problems 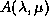 , whose solutions are typically
continua.
, whose solutions are typically
continua.



Next: Desired Spectral Information
Up: Mathematical Properties
Previous: What we plan
Jack Dongarra
Wed Jun 21 02:35:11 EDT 1995
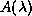
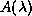
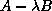 . These problems arise with
many kinds of special structures, many of which have been exploited in
special packages, some of them can be solved by general algorithms.
For example, solutions of Riccati equations are often
reduced to eigenproblems.
A comprehensive treatment of these problems would greatly expand the
scope of the book, but including some treatment seems important.
. These problems arise with
many kinds of special structures, many of which have been exploited in
special packages, some of them can be solved by general algorithms.
For example, solutions of Riccati equations are often
reduced to eigenproblems.
A comprehensive treatment of these problems would greatly expand the
scope of the book, but including some treatment seems important.
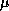 -analysis by its practitioners
These
problems must generally be solved by optimization techniques, and indeed
NP-completeness results exist for some of them. We believe that the
algorithms in our proposed book would be called within inner loops
for these optimization algorithms, and we should simply refer to the
literature for this application. The same comment applies for other
optimization problems based on eigenvalues (e.g. finding the nearest
unstable matrix).
-analysis by its practitioners
These
problems must generally be solved by optimization techniques, and indeed
NP-completeness results exist for some of them. We believe that the
algorithms in our proposed book would be called within inner loops
for these optimization algorithms, and we should simply refer to the
literature for this application. The same comment applies for other
optimization problems based on eigenvalues (e.g. finding the nearest
unstable matrix).
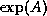 or
or 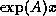 , or
for multivariate
eigenvalue problems
, or
for multivariate
eigenvalue problems 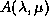 , whose solutions are typically
continua.
, whose solutions are typically
continua.