Notation



Next: Mathematical Properties
Up: Templates for Solution
Previous: Templates for Solution
- Matrix Pencil:
-
We will talk mostly about eigenproblems of the form
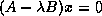 .
.
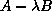 is also called a matrix pencil.
is also called a matrix pencil.
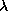 is an indeterminate in this latter expression,
and indicates that there are two matrices which define the eigenproblem.
is an indeterminate in this latter expression,
and indicates that there are two matrices which define the eigenproblem.
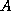 and
and 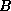 need not be square.
need not be square.
- Eigenvalues and Eigenvectors:
-
For almost all fixed scalar values of
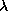 , the
rank of the matrix
, the
rank of the matrix 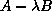 will be constant. The discrete set of values
of
will be constant. The discrete set of values
of
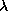 for which the rank of
for which the rank of 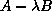 is lower than this constant are
the eigenvalues. Let
is lower than this constant are
the eigenvalues. Let 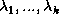 be the discrete set of
eigenvalues. Some
be the discrete set of
eigenvalues. Some 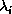 may be infinite, in which case we really consider
may be infinite, in which case we really consider
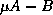 with eigenvalue
with eigenvalue 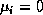 .
Nonzero vectors
.
Nonzero vectors 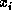 and
and 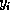 such that
such that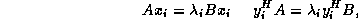
are called a right eigenvector and a left eigenvector,
respectively, where
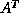 is the transpose of
is the transpose of 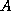 and
and 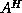 is its conjugate-transpose.
The word eigenvector alone will mean right eigenvector.
is its conjugate-transpose.
The word eigenvector alone will mean right eigenvector.
Since there are many kinds of eigenproblems, and associated algorithms, we
propose some simple top level categories to help classify them.
The ultimate decision tree presented to the reader will begin with easier
concepts and questions about the eigenproblem in an attempt to classify it,
and proceed to harder questions. For the purposes of this overview, we will
use rather more advanced categories in order to be brief but precise.
For background, see [12][25][23].
- Regular and Singular Pencils:
-
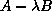 is regular if
is regular if
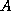 and
and 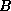 are square and
are square and 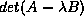 is not identically zero for all
is not identically zero for all 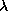 ; otherwise it
is singular.
; otherwise it
is singular.
Regular pencils have well-defined sets of eigenvalues
which change continuously as functions of 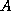 and
and 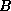 ;
this is a minimal requirement to be able to compute the
eigenvalues accurately, in the absence of other
constraints on
;
this is a minimal requirement to be able to compute the
eigenvalues accurately, in the absence of other
constraints on 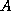 and
and 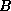 . Singular pencils have eigenvalues
which can change discontinuously as functions of
. Singular pencils have eigenvalues
which can change discontinuously as functions of
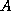 and
and 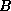 ; extra information about
; extra information about 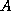 and
and 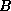 ,
as well as special algorithms which use this information,
are necessary in order to compute meaningful eigenvalues.
Regular and singular pencils have correspondingly different
canonical forms representing their spectral
decompositions. The Jordan Canonical Form of a single
matrix is the best known; the Kronecker Canonical Form
of a singular pencil is the most general. More will be
discussed in section 4.3
below.
,
as well as special algorithms which use this information,
are necessary in order to compute meaningful eigenvalues.
Regular and singular pencils have correspondingly different
canonical forms representing their spectral
decompositions. The Jordan Canonical Form of a single
matrix is the best known; the Kronecker Canonical Form
of a singular pencil is the most general. More will be
discussed in section 4.3
below.
- Self-adjoint and Non-self-adjoint Eigenproblems:
-
We abuse notation to avoid confusion with the very
similar but less general notions of Hermitian and non-Hermitian:
We call an eigenproblem
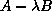 is self-adjoint if
1)
is self-adjoint if
1) 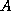 and
and 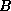 are both Hermitian, and
2) there is a nonsingular
are both Hermitian, and
2) there is a nonsingular  such that
such that 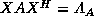 and
and
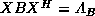 are real and diagonal.
Thus the finite eigenvalues are real, all elementary divisors
are linear, and the only possible singular blocks in the
Kronecker Canonical Form represent a common null space of
are real and diagonal.
Thus the finite eigenvalues are real, all elementary divisors
are linear, and the only possible singular blocks in the
Kronecker Canonical Form represent a common null space of
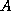 and
and 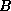 . The primary source of self-adjoint eigenproblems is
eigenvalue problems in which
. The primary source of self-adjoint eigenproblems is
eigenvalue problems in which 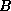 is known to be positive definite;
in this case
is known to be positive definite;
in this case 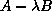 is called a definite pencil.
These properties lead to generally simpler and more
accurate algorithms. We classify the singular value decomposition (SVD)
and its generalizations as self-adjoint, because of the relationship
between the SVD of
is called a definite pencil.
These properties lead to generally simpler and more
accurate algorithms. We classify the singular value decomposition (SVD)
and its generalizations as self-adjoint, because of the relationship
between the SVD of 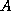 and the eigendecomposition of the Hermitian
matrix
and the eigendecomposition of the Hermitian
matrix  .
.
It is sometimes possible to change the classification of an eigenproblem
by simple transformations. For example, multiplying a skew-Hermitian
matrix 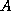 (i.e.,
(i.e., 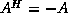 )
by the constant
)
by the constant 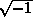 makes it Hermitian, so its
eigenproblem becomes self-adjoint. Such simple transformations are very
useful in finding the best algorithm for a problem.
makes it Hermitian, so its
eigenproblem becomes self-adjoint. Such simple transformations are very
useful in finding the best algorithm for a problem.
Many other definition and notation will be introduced in section
4.3.



Next: Mathematical Properties
Up: Templates for Solution
Previous: Templates for Solution
Jack Dongarra
Wed Jun 21 02:35:11 EDT 1995
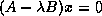 .
.
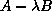 is also called a matrix pencil.
is also called a matrix pencil.
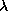 is an indeterminate in this latter expression,
and indicates that there are two matrices which define the eigenproblem.
is an indeterminate in this latter expression,
and indicates that there are two matrices which define the eigenproblem.
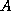 and
and 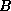 need not be square.
need not be square.
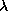 , the
rank of the matrix
, the
rank of the matrix 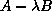 will be constant. The discrete set of values
of
will be constant. The discrete set of values
of
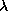 for which the rank of
for which the rank of 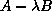 is lower than this constant are
the eigenvalues. Let
is lower than this constant are
the eigenvalues. Let 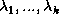 be the discrete set of
eigenvalues. Some
be the discrete set of
eigenvalues. Some 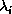 may be infinite, in which case we really consider
may be infinite, in which case we really consider
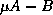 with eigenvalue
with eigenvalue 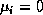 .
Nonzero vectors
.
Nonzero vectors 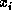 and
and 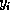 such that
such that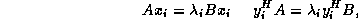
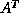 is the transpose of
is the transpose of 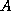 and
and 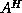 is its conjugate-transpose.
The word eigenvector alone will mean right eigenvector.
is its conjugate-transpose.
The word eigenvector alone will mean right eigenvector.
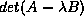 is not identically zero for all
is not identically zero for all  such that
such that 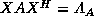 and
and
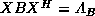 are real and diagonal.
Thus the finite eigenvalues are real, all elementary divisors
are linear, and the only possible singular blocks in the
Kronecker Canonical Form represent a common null space of
are real and diagonal.
Thus the finite eigenvalues are real, all elementary divisors
are linear, and the only possible singular blocks in the
Kronecker Canonical Form represent a common null space of
 .
.
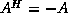 )
by the constant
)
by the constant 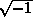 makes it Hermitian, so its
eigenproblem becomes self-adjoint. Such simple transformations are very
useful in finding the best algorithm for a problem.
makes it Hermitian, so its
eigenproblem becomes self-adjoint. Such simple transformations are very
useful in finding the best algorithm for a problem.