Notation

We use uppercase letters for matrices. The notation means that X has columns . The notation means that X has elements .

In general, we use lowercase Greek letters for scalars. Let

The following symbols have the indicated meaning

 mmmmmmmm¯

     		 The index space -- the set of values of the loop index vector

A 			 The matrix that transforms natural to new loop indices

  		 The matrix A with its columns scaled

        		     		 to have euclidean length one

F  			 

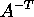
D  			 The matrix of dependences

C  			 The matrix of data fluxes

  		 The ratio of the volume of a tile to its surface area

		 The vector of block size parameters

		 A normal vector to a tiling hyperplane; one of the columns of A\

 			 A bound on the size of local memory.

		 The time required to perform the computation at a point

        		     		 in the index space.

		 The time required to move data across one unit of area

        		     		 in the hyperplane normal to .

We shall make considerable use of determinants. If is a real, square matrix, then the real-valued function is the volume of the parallelepiped subtended by the columns of X:

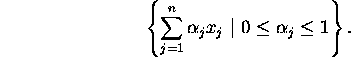
Thus, . Also . If Y is also , then . If is a triangular matrix, then .

Let denote the one-dimensional subspace spanned by the vector z, and let denote its orthogonal complement.

 
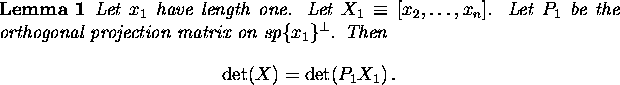
Proof: Let be a k-1-vector chosen so that for each , is orthogonal to . Construct the matrix

Then, since C is triangular and has unit diagonal, . Since is a vector of length one, . Thus,