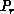We chose to use a Monte Carlo method to simulate the
interaction of the
particles. The method consists of generating a sequence of configurations in
such a way that the probability of being in configuration r, denoted as
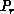, is
where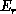 
is the potential energy of configuration r and 
.
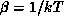A configuration refers collectively to the positions of all the particles in
the simulation. The update procedure that we describe in the next section
generates such a sequence of configurations by repeatedly updating the
position of each of the particles in the system. Averaging the values of
such quantities as potential energy and pressure over the configurations
gives their expected values in such a system.
The process of moving from one configuration to another is known as a Monte Carlo update. The update procedure we used involves three steps that allow the position of one particle to change [Metropolis:53a]. The first step is to choose a new position for the particle with uniform probability in a region about its current position. Next, the update procedure calculates the difference in potential energy between the current configuration and the new one. Finally, the new position for the particle is either accepted or rejected based on the difference in potential energy and rules that generate configurations with the required probability distribution.
The two-dimensional system being studied has several characteristics that
must be considered in designing an efficient algorithm for implementing the
Monte Carlo simulation. One of the most important characteristics is that
the interaction potential has a short range. The Lennard-Jones potential
approaches zero quickly enough that the effect of distant particles can be
safely ignored. We made the short-range nature of the potential precise by
truncating it at a distance of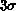 
. We must use the short-range nature
of the potential to organize the particle positions so that the update
procedure can quickly locate the particles whose potential energy changes
during an update.
Another feature of the system that complicates the simulation is that the
particles are not confined to a grid that would structure the data. Such
irregular data make simultaneously updating multiple particles more
difficult. One result of the irregular data is that the computational loads
of the processors are unbalanced in a distributed-memory, MIMD processor. In
order to minimize the effect of the load imbalance, the nodes of the
concurrent processor must run asynchronously. We developed an interrupt-driven
communication system [Johnson:85a] that allows the nodes to
implement an asynchronous update procedure. This ``rdsort''
system is described in Section 5.2.5 and has similarities to
the current active message ideas [Eiken:92a]. The
interrupt-driven communication system allows a node to send requests
for contributions to the change in potential energy that moving its
particle would cause. Nodes receiving such requests compute the
contribution of their particles and send a response reporting their
result. This operating system was sophisticated but only used for this
application. However, as described in Chapter 5, these ideas
formed the basis of both MOOS II and the evolution of CrOS III into
Express. Interestingly, Mark Johnson designed the loosely synchronous
CrOS III message-passing system as part of his service for C
P even
though his particular application was one of the few that could not
benefit from it.