




Next: Background on Markov
Up: An Improved Method
Previous: An Improved Method
In a local search method, one first defines a neighborhood topology on the set
of all tours. For instance, one might define the neighborhood of a tour
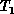 to be all those tours which can be obtained by changing at most k
edges of
to be all those tours which can be obtained by changing at most k
edges of 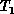 . A tour is said to be locally opt if no tour in its
neighborhood is shorter than it. One can search for locally opt tours by
starting with a random tour
. A tour is said to be locally opt if no tour in its
neighborhood is shorter than it. One can search for locally opt tours by
starting with a random tour 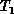 and performing k-changes on it as long
as the tour length decreases. In this way, one constructs a sequence of
tours
and performing k-changes on it as long
as the tour length decreases. In this way, one constructs a sequence of
tours 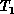 ,
, 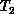 ,
,  . Eventually the process stops and one has
reached a local opt tour. Lin [Lin:65a] studied the case of k=2
and k=3, and showed that one could get quite good tours quickly.
Furthermore, since in general there are quite a few locally opt tours, in
order to find the globally optimal tour, he suggested repeating this process
from random starts many times until one was confident all the locally opt
tours had been found. Unfortunately, the number of local opt tours rises
exponentially with N, the number of cities. Thus in general, it is more
efficient to use a more sophisticated local opt (say higher k) than to try
to repeat the search from random starts many times. The current
state-of-the-art optimization heuristic is an algorithm due to Lin and
Kernighan [Lin:73a]. It is a variable depth k-neighborhood search,
and it is the benchmark against which all heuristics are tested. Since it is
significantly better than three-opt, for any instance of the TSP, there are
many fewer L-K-opt tours than there are three-opt tours. This
postpones the problem of doing exponentially many random starts until one
reaches N on the order of a few hundred. For still larger N, the number
of L-K-opt tours itself gets unmanageable. Given that one really does
want to tackle these larger problems, there are two natural ways to go.
First, one can try to extend the neighborhood which L-K considers, just
as L-K extended the neighborhood of three-changes. Second, one expects
that instead of sampling the local opt tours in a random way as is done by
applying the local searches from random starts many times, it might be
possible to obtain local opt tours in a more efficient way, say via a
sampling with a bias in favor of the shorter tours. We will see that this
gives rise to an algorithm which indeed enables one to solve much larger
instances.
. Eventually the process stops and one has
reached a local opt tour. Lin [Lin:65a] studied the case of k=2
and k=3, and showed that one could get quite good tours quickly.
Furthermore, since in general there are quite a few locally opt tours, in
order to find the globally optimal tour, he suggested repeating this process
from random starts many times until one was confident all the locally opt
tours had been found. Unfortunately, the number of local opt tours rises
exponentially with N, the number of cities. Thus in general, it is more
efficient to use a more sophisticated local opt (say higher k) than to try
to repeat the search from random starts many times. The current
state-of-the-art optimization heuristic is an algorithm due to Lin and
Kernighan [Lin:73a]. It is a variable depth k-neighborhood search,
and it is the benchmark against which all heuristics are tested. Since it is
significantly better than three-opt, for any instance of the TSP, there are
many fewer L-K-opt tours than there are three-opt tours. This
postpones the problem of doing exponentially many random starts until one
reaches N on the order of a few hundred. For still larger N, the number
of L-K-opt tours itself gets unmanageable. Given that one really does
want to tackle these larger problems, there are two natural ways to go.
First, one can try to extend the neighborhood which L-K considers, just
as L-K extended the neighborhood of three-changes. Second, one expects
that instead of sampling the local opt tours in a random way as is done by
applying the local searches from random starts many times, it might be
possible to obtain local opt tours in a more efficient way, say via a
sampling with a bias in favor of the shorter tours. We will see that this
gives rise to an algorithm which indeed enables one to solve much larger
instances.





Next: Background on Markov
Up: An Improved Method
Previous: An Improved Method
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
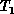 to be all those tours which can be obtained by changing at most k
edges of
to be all those tours which can be obtained by changing at most k
edges of 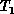 . A tour is said to be locally opt if no tour in its
neighborhood is shorter than it. One can search for locally opt tours by
starting with a random tour
. A tour is said to be locally opt if no tour in its
neighborhood is shorter than it. One can search for locally opt tours by
starting with a random tour 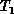 and performing k-changes on it as long
as the tour length decreases. In this way, one constructs a sequence of
tours
and performing k-changes on it as long
as the tour length decreases. In this way, one constructs a sequence of
tours 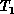 ,
, 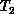 ,
,  . Eventually the process stops and one has
reached a local opt tour. Lin [Lin:65a] studied the case of k=2
and k=3, and showed that one could get quite good tours quickly.
Furthermore, since in general there are quite a few locally opt tours, in
order to find the globally optimal tour, he suggested repeating this process
from random starts many times until one was confident all the locally opt
tours had been found. Unfortunately, the number of local opt tours rises
exponentially with N, the number of cities. Thus in general, it is more
efficient to use a more sophisticated local opt (say higher k) than to try
to repeat the search from random starts many times. The current
state-of-the-art optimization heuristic is an algorithm due to Lin and
Kernighan [Lin:73a]. It is a variable depth k-neighborhood search,
and it is the benchmark against which all heuristics are tested. Since it is
significantly better than three-opt, for any instance of the TSP, there are
many fewer L-K-opt tours than there are three-opt tours. This
postpones the problem of doing exponentially many random starts until one
reaches N on the order of a few hundred. For still larger N, the number
of L-K-opt tours itself gets unmanageable. Given that one really does
want to tackle these larger problems, there are two natural ways to go.
First, one can try to extend the neighborhood which L-K considers, just
as L-K extended the neighborhood of three-changes. Second, one expects
that instead of sampling the local opt tours in a random way as is done by
applying the local searches from random starts many times, it might be
possible to obtain local opt tours in a more efficient way, say via a
sampling with a bias in favor of the shorter tours. We will see that this
gives rise to an algorithm which indeed enables one to solve much larger
instances.
. Eventually the process stops and one has
reached a local opt tour. Lin [Lin:65a] studied the case of k=2
and k=3, and showed that one could get quite good tours quickly.
Furthermore, since in general there are quite a few locally opt tours, in
order to find the globally optimal tour, he suggested repeating this process
from random starts many times until one was confident all the locally opt
tours had been found. Unfortunately, the number of local opt tours rises
exponentially with N, the number of cities. Thus in general, it is more
efficient to use a more sophisticated local opt (say higher k) than to try
to repeat the search from random starts many times. The current
state-of-the-art optimization heuristic is an algorithm due to Lin and
Kernighan [Lin:73a]. It is a variable depth k-neighborhood search,
and it is the benchmark against which all heuristics are tested. Since it is
significantly better than three-opt, for any instance of the TSP, there are
many fewer L-K-opt tours than there are three-opt tours. This
postpones the problem of doing exponentially many random starts until one
reaches N on the order of a few hundred. For still larger N, the number
of L-K-opt tours itself gets unmanageable. Given that one really does
want to tackle these larger problems, there are two natural ways to go.
First, one can try to extend the neighborhood which L-K considers, just
as L-K extended the neighborhood of three-changes. Second, one expects
that instead of sampling the local opt tours in a random way as is done by
applying the local searches from random starts many times, it might be
possible to obtain local opt tours in a more efficient way, say via a
sampling with a bias in favor of the shorter tours. We will see that this
gives rise to an algorithm which indeed enables one to solve much larger
instances.




