




Next: Single Residuals
Up: Single Integration Step
Previous: Single Integration Step
These computations of DASSL are a
fixed-leading-coefficient, variable-stepsize and -order,
backward-differentiation-formula (BDF) implicit integration scheme, described
clearly in [Brenan:89a, Chapter 5] and outlined in [Petzold:83a].
Concurrent DASSL faithfully implements this numerical method, with no
significant differences. Test problems run with the DASSL Fortran
code and the new C code (on one and multiple computers) certify this degree
of compatibility.
The sequential time complexity of the integration computations is 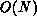 , if
considered separately from the residual calculation called in turn, which is
also normally
, if
considered separately from the residual calculation called in turn, which is
also normally 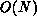 (see below). We pose these operations on a
(see below). We pose these operations on a
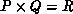 grid, where we assume that each process column can compute
complete residual vectors. Each process column repeats the entire prediction
operations: There is no speedup associated with Q > 1, and we replicate
all DASSL BDF and predictor vectors in each process column. Taller,
narrower grids are likely to provide the overall greatest speedup, though the
residual calculation may saturate (and slow down again) because of excessive
vertical communication requirements. It's definitely not true that the
grid, where we assume that each process column can compute
complete residual vectors. Each process column repeats the entire prediction
operations: There is no speedup associated with Q > 1, and we replicate
all DASSL BDF and predictor vectors in each process column. Taller,
narrower grids are likely to provide the overall greatest speedup, though the
residual calculation may saturate (and slow down again) because of excessive
vertical communication requirements. It's definitely not true that the
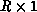 shape is optimal in all cases.
shape is optimal in all cases.
The distribution of coefficients in the rows has no impact on the integration
operations, and is dictated largely by the requirements of the residual
calculation itself. In practical problems, the concurrent database cannot be
reproduced in each process (cf., [Lorenz:92a]), so a given process
will only be able to compute some of the residuals. Furthermore, we may not
have complete freedom in scattering these equations, because there will often
be a trade-off between the degree of scattering and the amount of
communication needed to form the entire residual vector.
The amount of 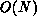 integration-computation work is not terribly
large-there is consequently a nontrivial but not tremendous effort
involved in the integration computations. (Residual computations
dominate in many if not most circumstances.) Integration operations
consist mainly of vector-vector operations not requiring any
interprocess communication and, in addition, fixed startup costs.
Operations include prediction of the solution at the time point,
initiation and control of the Newton iteration that ``corrects'' the
solution, convergence and error-tolerance checking,
and so forth. For example, the approximation
integration-computation work is not terribly
large-there is consequently a nontrivial but not tremendous effort
involved in the integration computations. (Residual computations
dominate in many if not most circumstances.) Integration operations
consist mainly of vector-vector operations not requiring any
interprocess communication and, in addition, fixed startup costs.
Operations include prediction of the solution at the time point,
initiation and control of the Newton iteration that ``corrects'' the
solution, convergence and error-tolerance checking,
and so forth. For example, the approximation 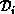 is chosen
within this block using the BDF formulas. For these operations, each
process column currently operates independently, and repetitively forms
the results. Alternatively, each process column could stride with step
Q, and row-combines could be used to propagate information
across the columns [Skjellum:90a]. This alternative would
increase speed for sufficiently large problems, and can easily be
implemented. However, because of load imbalance in other stages of the
calculation, we are convinced that including this type of
synchronization could be an overall negative rather than positive to
performance. This alternative will nevertheless be a future
user-selectable option.
is chosen
within this block using the BDF formulas. For these operations, each
process column currently operates independently, and repetitively forms
the results. Alternatively, each process column could stride with step
Q, and row-combines could be used to propagate information
across the columns [Skjellum:90a]. This alternative would
increase speed for sufficiently large problems, and can easily be
implemented. However, because of load imbalance in other stages of the
calculation, we are convinced that including this type of
synchronization could be an overall negative rather than positive to
performance. This alternative will nevertheless be a future
user-selectable option.
Included in these operations are a handful of norm operations, which
constitute the main interprocess communication required by the
integration computations step; norms are implemented concurrently via
recursive doubling (combine) [Stone:87a], [Skjellum:90a].
Actually, the weighted norm used by DASSL requires two recursive
doubling operations, each of which combines a scalar. The first
operation obtains the vector coefficient of maximum absolute value, the
second sums the weighted norm itself. Each can be implemented as Q
independent column combines, each producing the same repetitive result,
or a single Q-striding norm that takes advantage of the repetition of
information, but utilizes two combines over the entire process grid.
Both are supported in Concurrent DASSL, although the former is the
default norm. As with the original DASSL, the norm function can be
replaced, if desired.





Next: Single Residuals
Up: Single Integration Step
Previous: Single Integration Step
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
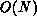 , if
considered separately from the residual calculation called in turn, which is
also normally
, if
considered separately from the residual calculation called in turn, which is
also normally 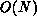 (see below). We pose these operations on a
(see below). We pose these operations on a
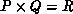 grid, where we assume that each process column can compute
complete residual vectors. Each process column repeats the entire prediction
operations: There is no speedup associated with Q > 1, and we replicate
all DASSL BDF and predictor vectors in each process column. Taller,
narrower grids are likely to provide the overall greatest speedup, though the
residual calculation may saturate (and slow down again) because of excessive
vertical communication requirements. It's definitely not true that the
grid, where we assume that each process column can compute
complete residual vectors. Each process column repeats the entire prediction
operations: There is no speedup associated with Q > 1, and we replicate
all DASSL BDF and predictor vectors in each process column. Taller,
narrower grids are likely to provide the overall greatest speedup, though the
residual calculation may saturate (and slow down again) because of excessive
vertical communication requirements. It's definitely not true that the
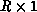 shape is optimal in all cases.
shape is optimal in all cases.





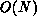 integration-computation work is not terribly
large-there is consequently a nontrivial but not tremendous effort
involved in the integration computations. (Residual computations
dominate in many if not most circumstances.) Integration operations
consist mainly of vector-vector operations not requiring any
interprocess communication and, in addition, fixed startup costs.
Operations include prediction of the solution at the time point,
initiation and control of the Newton iteration that ``corrects'' the
solution, convergence
integration-computation work is not terribly
large-there is consequently a nontrivial but not tremendous effort
involved in the integration computations. (Residual computations
dominate in many if not most circumstances.) Integration operations
consist mainly of vector-vector operations not requiring any
interprocess communication and, in addition, fixed startup costs.
Operations include prediction of the solution at the time point,
initiation and control of the Newton iteration that ``corrects'' the
solution, convergence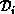 is chosen
within this block using the BDF formulas. For these operations, each
process column currently operates independently, and repetitively forms
the results. Alternatively, each process column could stride with step
Q, and row-combines could be used to propagate information
across the columns [
is chosen
within this block using the BDF formulas. For these operations, each
process column currently operates independently, and repetitively forms
the results. Alternatively, each process column could stride with step
Q, and row-combines could be used to propagate information
across the columns [