




Next: Evidence for the
Up: The Case of
Previous: The Case of
The quantum XY model was first proposed
[Matsubara:56a] in 1956 to study the lattice quantum fluids.
Later, high-temperature series studies raised the possibility of a
divergent susceptibility for the two-dimensional model. For the
classical planar model, the remarkable theory of Kosterlitz and
Thouless [Kosterlitz:73a] provided a clear physical picture and
correctly predicted a number of important properties. However, much
less is known about the quantum model. In fact, it has been
controversial. Using a large-order high-temperature expansion,
Rogiers, et al. [Rogiers:79a] suggested a second-order
transition at 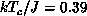 for spin-1/2. Later, real-space
renormalization group analysis was applied to the model with
contradictory and inconclusive results. DeRaedt, et al.
[DeRaedt:84a] then presented an exact solution and Monte Carlo
simulation, both based on the Suzuki-Trotter transformation with small
Trotter number m. Their results, both analytical and numerical,
supported an Ising-like (second-order) transition at the Ising
point
for spin-1/2. Later, real-space
renormalization group analysis was applied to the model with
contradictory and inconclusive results. DeRaedt, et al.
[DeRaedt:84a] then presented an exact solution and Monte Carlo
simulation, both based on the Suzuki-Trotter transformation with small
Trotter number m. Their results, both analytical and numerical,
supported an Ising-like (second-order) transition at the Ising
point 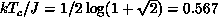 , with a logarithmically
divergent specific heat. Loh, et al. [Loh:85a] simulated
the system with an improved technique. They found that specific peak
remains finite and argued that a phase transition occurs at
, with a logarithmically
divergent specific heat. Loh, et al. [Loh:85a] simulated
the system with an improved technique. They found that specific peak
remains finite and argued that a phase transition occurs at
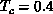 -0.5 by measuring the change of the ``twist energy'' from the
-0.5 by measuring the change of the ``twist energy'' from the
 lattice to the
lattice to the 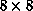 lattice. The dispute between
DeRaedt, et al., and Loh, et al., centered on the
importance of using a large Trotter number m and the global updates
in small-size systems, which move the system from one subspace to
another. Recent attempts to solve this problem still add fuel to the
controversy.
lattice. The dispute between
DeRaedt, et al., and Loh, et al., centered on the
importance of using a large Trotter number m and the global updates
in small-size systems, which move the system from one subspace to
another. Recent attempts to solve this problem still add fuel to the
controversy.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
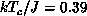 for spin-1/2. Later, real-space
renormalization group analysis was applied to the model with
contradictory and inconclusive results. DeRaedt, et al.
[DeRaedt:84a] then presented an exact solution and Monte Carlo
simulation, both based on the Suzuki-Trotter transformation with small
Trotter number m. Their results, both analytical and numerical,
supported an Ising-like (second-order) transition at the Ising
point
for spin-1/2. Later, real-space
renormalization group analysis was applied to the model with
contradictory and inconclusive results. DeRaedt, et al.
[DeRaedt:84a] then presented an exact solution and Monte Carlo
simulation, both based on the Suzuki-Trotter transformation with small
Trotter number m. Their results, both analytical and numerical,
supported an Ising-like (second-order) transition at the Ising
point 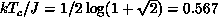 , with a logarithmically
divergent specific heat. Loh, et al. [Loh:85a] simulated
the system with an improved technique. They found that specific peak
remains finite and argued that a phase transition occurs at
, with a logarithmically
divergent specific heat. Loh, et al. [Loh:85a] simulated
the system with an improved technique. They found that specific peak
remains finite and argued that a phase transition occurs at
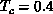 -0.5 by measuring the change of the ``twist energy'' from the
-0.5 by measuring the change of the ``twist energy'' from the
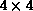 lattice to the
lattice to the 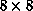 lattice. The dispute between
DeRaedt, et al., and Loh, et al., centered on the
importance of using a large Trotter number m and the global updates
in small-size systems, which move the system from one subspace to
another. Recent attempts to solve this problem still add fuel to the
controversy.
lattice. The dispute between
DeRaedt, et al., and Loh, et al., centered on the
importance of using a large Trotter number m and the global updates
in small-size systems, which move the system from one subspace to
another. Recent attempts to solve this problem still add fuel to the
controversy.




