- SRESID
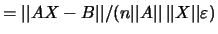
- FRESID
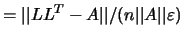
The Cholesky test program generates random symmetric test matrices with values in the interval [-1,1] and then modifies these matrices to be diagonally dominant with positive diagonal elements thus creating symmetric positive-definite matrices. It then calls the ScaLAPACK routines to factor and solve the system, and computes a solve and/or factorization residual error check to verify that each operation has performed correctly. Condition estimation and iterative refinement routines are included and optionally tested.
Specifically, each test matrix is subjected to the following tests:
The expert driver (PxPOSVX) performs condition estimation and iterative refinement and thus incorporates the following additional tests: