Previous: Nonstationary Iterative Methods
Up: Iterative Methods
Next: A short history of Krylov methods
Previous Page: Implementation
Next Page: A short history of Krylov methods

Summary of the Methods

Implementing an effective iterative method for solving a linear system cannot be done without some knowledge of the linear system. If good performance is important, consideration must also be given to the computational kernels of the method and how efficiently they can be executed on the target architecture. This point is of particular importance on parallel architectures; see §.

In this section we summarize for each method

• Matrix properties. Not every method will work on every problem type, so knowledge of matrix properties is the main criterion for selecting an iterative method.
• Computational kernels. Methods differ in the operations that they perform. However, the fact that one method uses more operations than another is not necessarily a reason for rejecting it.

  Moreover, it should be noted that for iterative methods applied to sparse systems of equations typically a lower performance is to be expected than for direct solution methods for dense systems. The sparsity of the matrix impedes reuse of data in the processor cache, and the indirect addressing of compressed storage schemes inhibits efficient pipelining of operations. Dongarra and Van der Vorst [71] give some experimental results about this, and provide a benchmark code for iterative solvers.

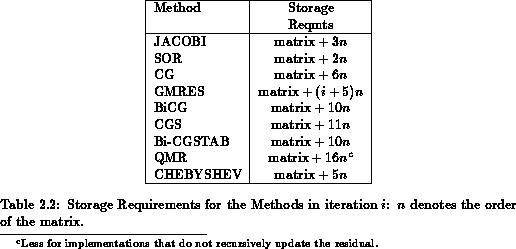
Table lists the storage required for each method (without preconditioning). Note that we are not including the original system and we ignore scalar storage.

1. Jacobi Method
   • Extremely easy to use, but unless the matrix is ``strongly'' diagonally dominant, this method is probably best only considered as an introduction to iterative methods or as a preconditioner in a nonstationary method.
   • Trivial to parallelize.
2. Gauss-Seidel Method
   • Typically faster convergence than Jacobi, but in general not competitive with the nonstationary methods.
   • Applicable to strictly diagonally dominant, or symmetric positive definite matrices.
   • Parallelization properties depend on structure of the coefficient matrix. Different orderings of the unknowns have different degrees of parallelism; multi-color orderings give almost full parallelism.
   • This is a special case of the SOR method, obtained by choosing .
3. Successive Over-Relaxation (SOR)
   • Accelerates convergence of Gauss-Seidel (, over-relaxation); may yield convergence when Gauss-Seidel fails (, under-relaxation).
   • Speed of convergence depends critically on ; the optimal value for may be estimated from the spectral radius of the Jacobi iteration matrix under certain conditions.
   • Parallelization properties are the same as those of the Gauss-Seidel method.
4. Conjugate Gradient (CG)
   • Applicable to symmetric positive definite systems.
   • Speed of convergence depends on the condition number; if extremal eigenvalues are well-separated then superlinear convergence behavior can result.
   • Inner products act as synchronization points in a parallel environment.
   • Further parallel properties are largely independent of the coefficient matrix, but depend strongly on the structure the preconditioner.
5. Generalized Minimal Residual (GMRES)
   • Applicable to nonsymmetric matrices.
   • GMRES leads to the smallest residual for a fixed number of iteration steps, but these steps become increasingly expensive.
   • In order to limit the increasing storage requirments and work per iteration step, restarting is necessary. When to do so depends on and the right-hand side; it requires skill and experience.
   • GMRES requires only matrix-vector products with the coefficient matrix.
   • The number of inner products grows linearly with the iteration number, up to the restart point. In an implementation based on a simple Gram-Schmidt process the inner products are independent, so together they imply only one synchronization point. A more stable implementation based on modified Gram-Schmidt orthogonalization has one synchronization point per inner product.
6. Biconjugate Gradient (BiCG)
   • Applicable to nonsymmetric matrices.
   • Requires matrix-vector products with the coefficient matrix and its transpose. This disqualifies the method for cases where the matrix is only implicitly given as an operator, and the transpose therefore not available at all.
   • Parallelization properties are similar to those for CG; the two matrix vector products (as well as the preconditioning steps) are independent, so they can be done in parallel, or their communication stages can be packaged.
7. Quasi-Minimal Residual (QMR)
   • Applicable to nonsymmetric matrices.
   • Designed to avoid the irregular convergence behavior of BiCG, it avoids one of the two breakdown situations of BiCG.
   • If BiCG makes significant progress in one iteration step, then QMR delivers about the same result at the same step. But when BiCG temporarily stagnates or diverges, QMR may still further reduce the residual, albeit very slowly.
   • Computational costs per iteration are similar to BiCG, but slightly higher. The method requires the transpose matrix-vector product.
   • Parallelization properties are as for BiCG.
8. Conjugate Gradient Squared (CGS)
   • Applicable to nonsymmetric matrices.
   • Converges (diverges) typically about twice as fast as BiCG.
   • Convergence behavior is often quite irregular, which may lead to a loss of accuracy in the updated residual. Tends to diverge if the starting guess is close to the solution.
   • Computational costs per iteration are similar to BiCG, but the method doesn't require the transpose matrix.
   • Unlike BiCG, the two matrix-vector products are not independent, so the number of synchronization points in a parallel environment is larger.
9. Biconjugate Gradient Stabilized (Bi-CGSTAB)
   • Applicable to nonsymmetric matrices.
   • Computational costs per iteration are similar to BiCG and CGS, but the method doesn't require the transpose matrix.
   • An alternative for CGS that avoids the irregular convergence patterns of CGS while maintaining about the same speed of convergence; as a result we observe often less loss of accuracy in the updated residual.
10. Chebyshev Iteration
    • Applicable to nonsymmetric matrices (but presented in this book only for the symmetric case).
    • This method requires some explicit knowledge of the spectrum (or field of values); in the symmetric case the iteration parameters are easily obtained from the two extremal eigenvalues, which can be estimated either directly from the matrix, or from applying a few iterations of the Conjugate Gradient Method.
    • The computational structure is similar to that of CG, but there are no synchronization points.
    • The Adaptive Chebyshev method can be used in combination with methods as CG or GMRES, to continue the iteration once suitable bounds on the spectrum have been obtained from these methods.

Selecting the ``best'' method for a given class of problems is largely a matter of trial and error. It also depends on how much storage one has available (GMRES), on the availability of (BiCG and QMR), and on how expensive the matrix vector products (and Solve steps with ) are in comparison to SAXPYs and inner products. If these matrix vector products are relatively expensive, and if sufficient storage is available then it may be attractive to use GMRES and delay restarting as much as possible.

Table shows the type of operations performed per iteration. Based on the particular problem or data structure, the user may observe that a particular operation could be performed more efficiently.