CDS Matrix-Vector Product





Next: Sparse Incomplete Factorizations
Up: Matrix vector products
Previous: CRS Matrix-Vector Product
If the 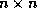 matrix
matrix 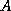 is
stored in CDS format, it is still possible to
perform a matrix-vector product
is
stored in CDS format, it is still possible to
perform a matrix-vector product 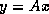 by either rows or columns, but this
does not take advantage of the CDS format. The idea
is to make a change in coordinates in the doubly-nested loop. Replacing
by either rows or columns, but this
does not take advantage of the CDS format. The idea
is to make a change in coordinates in the doubly-nested loop. Replacing
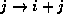 we get
we get
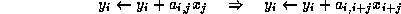
With the index 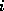 in the inner loop we see that the
expression
in the inner loop we see that the
expression 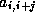 accesses the
accesses the 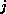 th diagonal of the matrix
(where the main diagonal has number 0).
th diagonal of the matrix
(where the main diagonal has number 0).
The algorithm will now have a doubly-nested loop with the outer loop
enumerating the diagonals diag=-p,q with 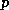 and
and 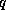 the
(nonnegative) numbers of diagonals to the left and right of the main
diagonal. The bounds for the inner loop follow from the requirement
that
the
(nonnegative) numbers of diagonals to the left and right of the main
diagonal. The bounds for the inner loop follow from the requirement
that

The algorithm becomes
for i = 1, n
y(i) = 0
end;
for diag = -diag_left, diag_right
for loc = max(1,1-diag), min(n,n-diag)
y(loc) = y(loc) + val(loc,diag) * x(loc+diag)
end;
end;
The transpose matrix-vector product 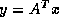 is a minor variation of the
algorithm above. Using the update formula
is a minor variation of the
algorithm above. Using the update formula

we obtain
for i = 1, n
y(i) = 0
end;
for diag = -diag_right, diag_left
for loc = max(1,1-diag), min(n,n-diag)
y(loc) = y(loc) + val(loc+diag, -diag) * x(loc+diag)
end;
end;
The memory access for the CDS-based matrix-vector product 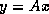 (or
(or 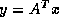 ) is
three vectors per inner iteration. On the other hand, there is no
indirect addressing, and the algorithm is vectorizable with vector
lengths of essentially the matrix order
) is
three vectors per inner iteration. On the other hand, there is no
indirect addressing, and the algorithm is vectorizable with vector
lengths of essentially the matrix order  . Because of the regular data
access, most machines can perform this algorithm
efficiently by keeping three base registers and using simple offset
addressing.
. Because of the regular data
access, most machines can perform this algorithm
efficiently by keeping three base registers and using simple offset
addressing.
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
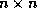 matrix
matrix 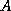 is
stored in CDS format, it is still possible to
perform a matrix-vector product
is
stored in CDS format, it is still possible to
perform a matrix-vector product 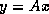 by either rows or columns, but this
does not take advantage of the CDS format. The idea
is to make a change in coordinates in the doubly-nested loop. Replacing
by either rows or columns, but this
does not take advantage of the CDS format. The idea
is to make a change in coordinates in the doubly-nested loop. Replacing
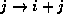 we get
we get
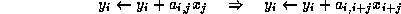
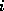 in the inner loop we see that the
expression
in the inner loop we see that the
expression 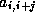 accesses the
accesses the 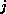 th diagonal of the matrix
(where the main diagonal has number 0).
th diagonal of the matrix
(where the main diagonal has number 0).
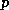 and
and 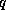 the
(nonnegative) numbers of diagonals to the left and right of the main
diagonal. The bounds for the inner loop follow from the requirement
that
the
(nonnegative) numbers of diagonals to the left and right of the main
diagonal. The bounds for the inner loop follow from the requirement
that 
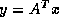 is a minor variation of the
algorithm above. Using the update formula
is a minor variation of the
algorithm above. Using the update formula

 . Because of the regular data
access, most machines can perform this algorithm
efficiently by keeping three base registers and using simple offset
addressing.
. Because of the regular data
access, most machines can perform this algorithm
efficiently by keeping three base registers and using simple offset
addressing.