Polynomial preconditioners





Next: Preconditioners from properties
Up: Preconditioners
Previous: Incomplete LQ factorizations
So far, we have described preconditioners in only one of two classes:
those that approximate the coefficient
matrix, and where linear systems with the preconditioner as
coefficient matrix are easier to solve than the original system.
Polynomial preconditioners can be considered as members of the
second class of preconditioners:
direct approximations of the inverse of the coefficient matrix.
Suppose that the coefficient matrix  of the linear system is
normalized to
the form
of the linear system is
normalized to
the form 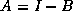 , and that the spectral radius of
, and that the spectral radius of 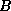 is less than
one. Using the Neumann series, we can write the inverse of
is less than
one. Using the Neumann series, we can write the inverse of  as
as
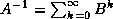 ,
so an approximation may be derived by truncating this infinite series.
Since the iterative methods we are considering are already based on
the idea of applying polynomials in the coefficient matrix to the
initial residual, there are analytic connections between the basic
method and polynomially accelerated one.
,
so an approximation may be derived by truncating this infinite series.
Since the iterative methods we are considering are already based on
the idea of applying polynomials in the coefficient matrix to the
initial residual, there are analytic connections between the basic
method and polynomially accelerated one.
Dubois, Greenbaum and Rodrigue [77]
investigated the relationship between a basic method
using a splitting 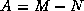 , and a polynomially preconditioned method
with
, and a polynomially preconditioned method
with
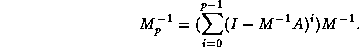
The basic result is that for classical methods,
 steps of the polynomially preconditioned method are
exactly equivalent to
steps of the polynomially preconditioned method are
exactly equivalent to
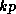 steps of the original method; for accelerated
methods, specifically the Chebyshev method, the preconditioned
iteration can improve the number of iterations by at most a factor
of
steps of the original method; for accelerated
methods, specifically the Chebyshev method, the preconditioned
iteration can improve the number of iterations by at most a factor
of 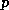 .
.
Although there is no gain in the number of times the coefficient
matrix is applied, polynomial preconditioning does eliminate a large
fraction of the inner
products and update operations, so there may be an overall increase in
efficiency.
Let us define a polynomial preconditioner more abstractly as any
polynomial 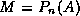 normalized to
normalized to 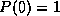 . Now the choice of the
best polynomial preconditioner becomes that of choosing the best
polynomial that minimizes
. Now the choice of the
best polynomial preconditioner becomes that of choosing the best
polynomial that minimizes 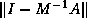 . For the choice of the
infinity norm we thus obtain Chebyshev polynomials, and they require
estimates of both a lower and upper bound on the spectrum of
. For the choice of the
infinity norm we thus obtain Chebyshev polynomials, and they require
estimates of both a lower and upper bound on the spectrum of  .
These estimates may be derived from the conjugate gradient iteration
itself; see §
.
These estimates may be derived from the conjugate gradient iteration
itself; see § .
.
Since an accurate lower bound on the spectrum of  may be hard to
obtain, Johnson, Micchelli and Paul [126]
and Saad [183] propose least
squares polynomials based on several weight functions.
These functions only require an upper bound and this is easily
computed, using for instance the ``Gerschgorin bound''
may be hard to
obtain, Johnson, Micchelli and Paul [126]
and Saad [183] propose least
squares polynomials based on several weight functions.
These functions only require an upper bound and this is easily
computed, using for instance the ``Gerschgorin bound''
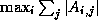 ; see [.4]Va:book.
Experiments comparing Chebyshev and least squares polynomials can be
found in Ashby, Manteuffel and Otto [8].
; see [.4]Va:book.
Experiments comparing Chebyshev and least squares polynomials can be
found in Ashby, Manteuffel and Otto [8].
Application of polynomial preconditioning to symmetric indefinite
problems is described by Ashby, Manteuffel and
Saylor [9]. There the
polynomial is chosen so that it transforms the system into a
definite one.





Next: Preconditioners from properties
Up: Preconditioners
Previous: Incomplete LQ factorizations
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
 of the linear system is
normalized to
the form
of the linear system is
normalized to
the form 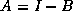 , and that the spectral radius of
, and that the spectral radius of 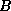 is less than
one. Using the Neumann series, we can write the inverse of
is less than
one. Using the Neumann series, we can write the inverse of  as
as
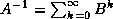 ,
so an approximation may be derived by truncating this infinite series.
Since the iterative methods we are considering are already based on
the idea of applying polynomials in the coefficient matrix to the
initial residual, there are analytic connections between the basic
method and polynomially accelerated one.
,
so an approximation may be derived by truncating this infinite series.
Since the iterative methods we are considering are already based on
the idea of applying polynomials in the coefficient matrix to the
initial residual, there are analytic connections between the basic
method and polynomially accelerated one.
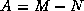 , and a polynomially preconditioned method
with
, and a polynomially preconditioned method
with
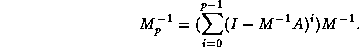
 steps of the polynomially preconditioned method are
exactly equivalent to
steps of the polynomially preconditioned method are
exactly equivalent to
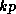 steps of the original method; for accelerated
methods, specifically the Chebyshev method, the preconditioned
iteration can improve the number of iterations by at most a factor
of
steps of the original method; for accelerated
methods, specifically the Chebyshev method, the preconditioned
iteration can improve the number of iterations by at most a factor
of 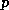 .
.
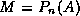 normalized to
normalized to 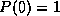 . Now the choice of the
best polynomial preconditioner becomes that of choosing the best
polynomial that minimizes
. Now the choice of the
best polynomial preconditioner becomes that of choosing the best
polynomial that minimizes 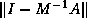 . For the choice of the
infinity norm we thus obtain Chebyshev polynomials, and they require
estimates of both a lower and upper bound on the spectrum of
. For the choice of the
infinity norm we thus obtain Chebyshev polynomials, and they require
estimates of both a lower and upper bound on the spectrum of 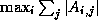 ; see [.4]Va:book.
Experiments comparing Chebyshev and least squares polynomials can be
found in Ashby, Manteuffel and Otto
; see [.4]Va:book.
Experiments comparing Chebyshev and least squares polynomials can be
found in Ashby, Manteuffel and Otto