




Next: Arguments
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: LA_GGEVX
Contents
Index
LA_GGEVX computes for a pair of 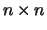 real or complex matrices
real or complex matrices 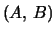 the generalized eigenvalues in the form of scalar pairs (
the generalized eigenvalues in the form of scalar pairs (
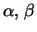 )
and, optionally, the left and/or right generalized eigenvectors.
)
and, optionally, the left and/or right generalized eigenvectors.
A generalized eigenvalue of the pair 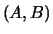 is, roughly speaking, a
scalar of the form
is, roughly speaking, a
scalar of the form
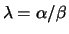 such that the matrix
such that the matrix
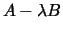 is singular. It is usually represented as the pair
is singular. It is usually represented as the pair
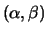 , as
there is a reasonable interpretation of the case
, as
there is a reasonable interpretation of the case 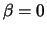 (even if
(even if 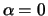 ).
).
A right generalized eigenvector corresponding to a generalized
eigenvalue 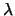 is a vector
is a vector 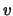 such
that
such
that
 . A left generalized eigenvector is
a vector
. A left generalized eigenvector is
a vector 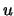 such that
such that
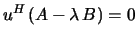 , where
, where 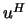 is
the conjugate-transpose of
is
the conjugate-transpose of 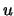 .
.
The computation is based on the (generalized) real or complex Schur form of
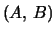 . (See LA_GGES for details of this form.)
. (See LA_GGES for details of this form.)
Optionally, LA_GGEVX also computes a balancing transformation (to improve
the conditioning of the eigenvalues and eigenvectors), reciprocal
condition numbers for the eigenvalues, and reciprocal condition numbers for the
right eigenvectors. The balancing transformation consists of a permutation of
rows and columns and/or a scaling of rows and columns.





Next: Arguments
Up: Generalized Nonsymmetric Eigenvalue Problems
Previous: LA_GGEVX
Contents
Index
Susan Blackford
2001-08-19