Further Details: Error Bounds for the Singular Value Decomposition





Next: Error Bounds for
Up: Error Bounds for
Previous: Error Bounds for
The usual error analysis of the SVD algorithm
xGESVD in LAPACK (see
subsection 2.2.4) or the
routines in LINPACK and EISPACK is as follows [45]:
The SVD algorithm is backward stable.
This means that the computed SVD, 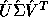 ,
is nearly the exact SVD of A + E where
,
is nearly the exact SVD of A + E where 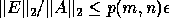 ,
and p(m , n) is a modestly growing function of m and n. This means
,
and p(m , n) is a modestly growing function of m and n. This means
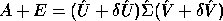 is the true SVD, so that
is the true SVD, so that 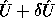 and
and 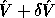 are both orthogonal, where
are both orthogonal, where
 , and
, and
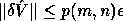 .
Each computed singular value
.
Each computed singular value 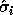 differs from true
differs from true 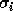 by at most
by at most
(we take p(m , n) = 1 in the code fragment).
Thus large singular values (those near 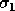 ) are computed to
high relative accuracy and small ones may not be.
) are computed to
high relative accuracy and small ones may not be.
The angular difference between the computed left singular vector 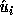 and a true
and a true 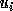 satisfies the approximate bound
satisfies the approximate bound

where 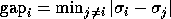 is the
absolute gap
between
is the
absolute gap
between 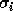 and the nearest other singular value.
We take p(m , n) = 1 in the code fragment.
Thus, if
and the nearest other singular value.
We take p(m , n) = 1 in the code fragment.
Thus, if 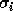 is close to other singular values, its corresponding singular vector
is close to other singular values, its corresponding singular vector 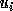 may be inaccurate. When n > m, then
may be inaccurate. When n > m, then 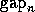 must be redefined
as
must be redefined
as 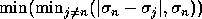 .
The gaps may be easily computed from the array of computed singular values
using function SDISNA.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
The same bound applies to the computed right singular
vector
.
The gaps may be easily computed from the array of computed singular values
using function SDISNA.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
The same bound applies to the computed right singular
vector 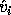 and a true vector
and a true vector 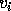 .
.
Let 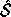 be the space spanned by a collection of computed left singular
vectors
be the space spanned by a collection of computed left singular
vectors 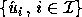 , where
, where 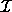 is a subset
of the integers from 1 to n. Let S be the corresponding true space.
Then
is a subset
of the integers from 1 to n. Let S be the corresponding true space.
Then
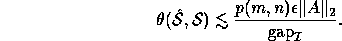
where
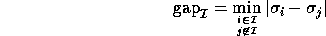
is the absolute gap between the singular values in 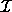 and the nearest
other singular value. Thus, a cluster
of close singular values which is
far away from any other singular value may have a well determined
space
and the nearest
other singular value. Thus, a cluster
of close singular values which is
far away from any other singular value may have a well determined
space 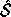 even if its individual singular vectors are ill-conditioned.
The same bound applies to a set of right singular vectors
even if its individual singular vectors are ill-conditioned.
The same bound applies to a set of right singular vectors
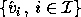
 .
.
In the special case of bidiagonal matrices, the singular values and
singular vectors may be computed much more accurately. A bidiagonal
matrix B has nonzero entries only on the main diagonal and the diagonal
immediately
above it (or immediately below it). xGESVD computes the SVD of a general
matrix by first reducing it to bidiagonal form B, and then calling xBDSQR
(subsection 2.3.6)
to compute the SVD of B.
Reduction of a dense matrix to bidiagonal form B can introduce
additional errors, so the following bounds for the bidiagonal case
do not apply to the dense case.
Each computed singular value of a bidiagonal matrix
is accurate to nearly full relative accuracy ,
no matter how tiny it is: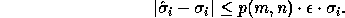
The computed left singular vector 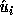 has an angular error
at most about
has an angular error
at most about
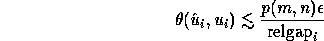
where
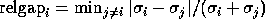 is the relative gap between
is the relative gap between 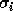 and the nearest other singular
value. The same bound applies to the right singular vector
and the nearest other singular
value. The same bound applies to the right singular vector 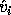 and
and 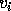 .
Since the relative gap may be much larger than
the absolute gap ,
this error bound may be much smaller than the previous one. The relative gaps
may be easily computed from the array of computed singular values.
.
Since the relative gap may be much larger than
the absolute gap ,
this error bound may be much smaller than the previous one. The relative gaps
may be easily computed from the array of computed singular values.
In the very special case of 2-by-2 bidiagonal matrices, xBDSQR
calls auxiliary routine xLASV2 to compute the SVD. xLASV2 will
actually compute nearly correctly rounded singular vectors independent of
the relative gap, but this requires accurate computer arithmetic:
if leading digits cancel during floating-point subtraction, the resulting
difference must be exact.
On machines without guard digits one has the slightly weaker result that the
algorithm is componentwise relatively backward stable, and therefore the
accuracy of the singular vectors depends on the relative gap as described
above.
Jacobi's method [69][76][24] is another
algorithm for finding singular values and singular vectors of matrices.
It is slower than the algorithms based on first tridiagonalizing the matrix,
but is capable of computing more accurate answers in several important cases.
Routines implementing Jacobi's method and corresponding error bounds will be
available in a future LAPACK release.





Next: Error Bounds for
Up: Error Bounds for
Previous: Error Bounds for
Tue Nov 29 14:03:33 EST 1994
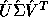 ,
is nearly the exact SVD of A + E where
,
is nearly the exact SVD of A + E where 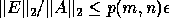 ,
and p(m , n) is a modestly growing function of m and n. This means
,
and p(m , n) is a modestly growing function of m and n. This means
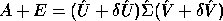 is the true SVD, so that
is the true SVD, so that 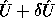 and
and 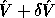 are both orthogonal, where
are both orthogonal, where
 , and
, and
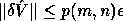 .
Each computed singular value
.
Each computed singular value 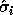 differs from true
differs from true 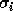 by at most
by at most
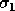 ) are computed to
high relative accuracy and small ones may not be.
) are computed to
high relative accuracy and small ones may not be.
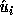 and a true
and a true 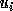 satisfies the approximate bound
satisfies the approximate bound
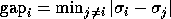 is the
absolute gap
between
is the
absolute gap
between 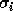 and the nearest other singular value.
We take p(m , n) = 1 in the code fragment.
Thus, if
and the nearest other singular value.
We take p(m , n) = 1 in the code fragment.
Thus, if 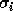 is close to other singular values, its corresponding singular vector
is close to other singular values, its corresponding singular vector 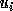 may be inaccurate. When n > m, then
may be inaccurate. When n > m, then 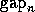 must be redefined
as
must be redefined
as 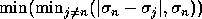 .
The gaps may be easily computed from the array of computed singular values
using function SDISNA.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
The same bound applies to the computed right singular
vector
.
The gaps may be easily computed from the array of computed singular values
using function SDISNA.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
The same bound applies to the computed right singular
vector 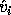 and a true vector
and a true vector 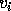 .
.
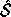 be the space spanned by a collection of computed left singular
vectors
be the space spanned by a collection of computed left singular
vectors 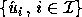 , where
, where 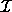 is a subset
of the integers from 1 to n. Let S be the corresponding true space.
Then
is a subset
of the integers from 1 to n. Let S be the corresponding true space.
Then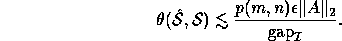
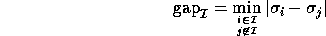
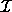 and the nearest
other singular value. Thus, a cluster
of close singular values which is
far away from any other singular value may have a well determined
space
and the nearest
other singular value. Thus, a cluster
of close singular values which is
far away from any other singular value may have a well determined
space 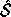 even if its individual singular vectors are ill-conditioned.
The same bound applies to a set of right singular vectors
even if its individual singular vectors are ill-conditioned.
The same bound applies to a set of right singular vectors
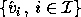
![]() .
.
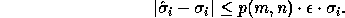
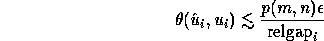
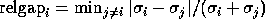 is the relative gap between
is the relative gap between