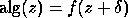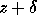We illustrate standard error analysis with the simple example of
evaluating the scalar function y = f(z). Let the output of the
subroutine which implements f(z) be denoted alg(z); this includes
the effects of roundoff. If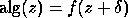 
where 
is small,
then we say alg is a backward stable
algorithm for f,
or that the backward error is small.
In other words, alg(z) is the
exact value of f at a slightly perturbed input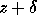 
.
Suppose now that f is a smooth function, so that
we may approximate it near z by a straight line:
.
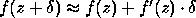Then we have the simple error estimate
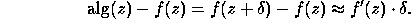
Thus, if is small, and the derivative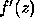 
is
moderate, the error alg(z) - f(z) will be small.
This is often written
in the similar form
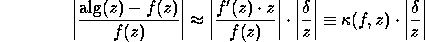
This approximately bounds the relative error
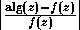by the product of
the condition number of
f at z,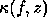 
, and the
relative backward error 
.
Thus we get an error bound by multiplying a
condition number and
a backward error (or bounds for these quantities). We call a problem
ill-conditioned if its condition number is large,
and ill-posed
if its condition number is infinite (or does not exist).
If f and z are vector quantities, then 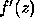is a matrix
(the Jacobian). So instead of using absolute values as before,
we now measure by a vector norm 
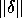and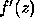
by a matrix norm 
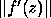. The conventional (and coarsest) error analysis
uses a norm such as the infinity norm. We therefore call
this normwise backward stability.
For example, a normwise stable
method for solving a system of linear equations Ax = b will
produce a solution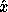 
satisfying 
where
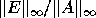and
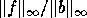are both small (close to machine epsilon).
In this case the condition number is
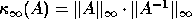(see section 4.4 below).
Almost all of the algorithms in LAPACK (as well as LINPACK and EISPACK)
are stable in the sense just described:
when applied to a matrix A
they produce the exact result for a slightly different matrix A + E,
where 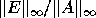is of order 
.
Condition numbers may be expensive to compute
exactly.
For example, it costs about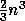 
operations to solve Ax = b
for a general matrix A, and computing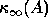 
exactly costs
an additional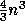 
operations, or twice as much.
But 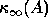can be estimated in only 
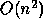operations beyond those 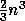necessary for solution,
a tiny extra cost. Therefore, most of LAPACK's condition numbers
and error bounds are based on estimated condition
numbers , using the method
of [52][51][48].
The price one pays for using an estimated rather than an
exact condition number is occasional
(but very rare) underestimates of the true error; years of experience
attest to the reliability of our estimators, although examples
where they badly underestimate the error can be constructed [53].
Note that once a condition estimate is large enough,
(usually 
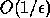), it confirms that the computed
answer may be completely inaccurate, and so the exact magnitude
of the condition estimate conveys little information.