The eigendecomposition of
an n-by-n real symmetric matrix is the
factorization
![]() (
(
![]() in the complex Hermitian
case), where Z is orthogonal (unitary) and
in the complex Hermitian
case), where Z is orthogonal (unitary) and
![]() is real and diagonal,
with
is real and diagonal,
with
![]() .
The
.
The ![]() are the eigenvalues of A and the columns zi of
Z are the eigenvectors. This is also often written
are the eigenvalues of A and the columns zi of
Z are the eigenvectors. This is also often written
![]() .
The eigendecomposition of a symmetric matrix is
computed
by the driver routines
xSYEV, xSYEVX, xSYEVD, xSYEVR,
xSBEV, xSBEVX, xSBEVD,
xSPEV, xSPEVX, xSPEVD,
xSTEV, xSTEVX, xSTEVD and xSTEVR.
The complex counterparts of these routines, which compute the
eigendecomposition of complex Hermitian matrices, are
the driver routines
xHEEV, xHEEVX, xHEEVD, xHEEVR,
xHBEV, xHBEVX, xHBEVD,
xHPEV, xHPEVX, and xHPEVD
(see subsection 2.3.4).
.
The eigendecomposition of a symmetric matrix is
computed
by the driver routines
xSYEV, xSYEVX, xSYEVD, xSYEVR,
xSBEV, xSBEVX, xSBEVD,
xSPEV, xSPEVX, xSPEVD,
xSTEV, xSTEVX, xSTEVD and xSTEVR.
The complex counterparts of these routines, which compute the
eigendecomposition of complex Hermitian matrices, are
the driver routines
xHEEV, xHEEVX, xHEEVD, xHEEVR,
xHBEV, xHBEVX, xHBEVD,
xHPEV, xHPEVX, and xHPEVD
(see subsection 2.3.4).
The approximate error
bounds4.10
for the computed eigenvalues
![]() are
are
EPSMCH = SLAMCH( 'E' )
* Compute eigenvalues and eigenvectors of A
* The eigenvalues are returned in W
* The eigenvector matrix Z overwrites A
CALL SSYEV( 'V', UPLO, N, A, LDA, W, WORK, LWORK, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'SSYEV did not converge'
ELSE IF ( N.GT.0 ) THEN
* Compute the norm of A
ANORM = MAX( ABS( W(1) ), ABS( W(N) ) )
EERRBD = EPSMCH * ANORM
* Compute reciprocal condition numbers for eigenvectors
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
ZERRBD( I ) = EPSMCH * ( ANORM / RCONDZ( I ) )
10 CONTINUE
ENDIF
For example4.11,
if
![]() and
and
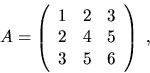
| i |
|
EERRBD | true
|
ZERRBD(i) | true
|
| 1 | -.5157 |
|
|
|
|
| 2 | .1709 |
|
|
|
|
| 3 | 11.34 |
|
|
|
|