




Next: Summary of Choices.
Up: Introduction
Previous: Introduction
Contents
Index
The reader might remember that eigenvalue problems of moderate size,
which in this case means that a full  matrix can be
stored conveniently, are solved by
direct methods, sometimes also called
transformation methods, where similarity transformations
are applied until the eigenvalues can be easily
read out.
matrix can be
stored conveniently, are solved by
direct methods, sometimes also called
transformation methods, where similarity transformations
are applied until the eigenvalues can be easily
read out.![[*]](http://www.netlib.org/utk/icons/footnote.png) We give a short
review of some current direct methods in §4.2.
We give a short
review of some current direct methods in §4.2.
The main emphasis in this book is on iterative methods where
sparse matrix storage can be used to advantage. Here
the matrix operator is applied to one or a few starting vectors, eigenvalue
approximations are computed from subspaces of low dimension,
and the iteration is continued until convergence to a subset of the
eigenvalues is indicated.
Six basic iterative algorithms will be described in this chapter:
- Power method,
- described in §4.3, is
the basic iterative method. It takes a starting vector and lets
the matrix operate on it until we get vectors that are parallel
to the leading eigenvector. It converges when there is one unique
eigenvalue of largest magnitude, but even in these favorable cases
it is slower than other algorithms discussed in this chapter.
- Subspace iteration method,
- sometimes also
called simultaneous iteration, and described in §4.3,
lets the matrix operate on a set of vectors simultaneously, until the
iterated vectors span the invariant subspace of the leading eigenvalues.
It is the basis of several structural engineering software packages
and has a simple implementation and theory of convergence to recommend it.
It is, however, slower to converge than algorithms based on
Lanczos orthogonalization.
- Lanczos method,
- §4.4,
builds up an orthogonal basis of the Krylov sequence of vectors
produced by repeated application of the matrix
 to a starting vector.
In this orthogonal basis, the matrix operator is represented by a
tridiagonal matrix
to a starting vector.
In this orthogonal basis, the matrix operator is represented by a
tridiagonal matrix 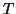 , whose eigenvalues yield Ritz approximations
to several of the eigenvalues of the original matrix
, whose eigenvalues yield Ritz approximations
to several of the eigenvalues of the original matrix  . Its main advantage,
compared to the power method, is that it yields approximations to
several eigenvalues from one sequence of vectors and that these converge
after much fewer matrix-vector multiplications. On the other hand,
there are potential complications: even if a simple three-term recurrence is
enough to give a mathematically orthogonal basis, rounding errors
will destroy orthogonality as soon as the first eigenvalue
converges, and one has to apply some kind of reorthogonalization.
If one needs only eigenvalues, the Lanczos algorithm is economical
in storage space.
We will describe some variants in §4.4.
. Its main advantage,
compared to the power method, is that it yields approximations to
several eigenvalues from one sequence of vectors and that these converge
after much fewer matrix-vector multiplications. On the other hand,
there are potential complications: even if a simple three-term recurrence is
enough to give a mathematically orthogonal basis, rounding errors
will destroy orthogonality as soon as the first eigenvalue
converges, and one has to apply some kind of reorthogonalization.
If one needs only eigenvalues, the Lanczos algorithm is economical
in storage space.
We will describe some variants in §4.4.
- Implicitly restarted Lanczos method,
- §4.5, is a variant
where the size of the orthogonal basis is kept bounded and continuously
updated, until its subspace contains a prescribed set of eigenvectors.
In many cases, it can get the same number of eigenvalues to converge
as the original variant of Lanczos, using only marginally more matrix-vector
multiplications but significantly less storage space.
This variant is especially useful if one needs eigenvectors.
- Band Lanczos method,
- §4.6, is the Lanczos counterpart
of the simultaneous power method. For matrices stored on backing storage,
or in a memory hierarchy, it is much more efficient to operate on
several vectors simultaneously than on one after the other.
This is the reason that several state-of-the-art structural
engineering packages use this kind of algorithm [206].
In multiple-input multiple-output control problems, one is actually
interested in reduced-order models based on a given set of starting vectors,
which is the main reason to develop the variant described here.
- Jacobi-Davidson method,
- §4.7, is a development
of an algorithm that is popular in quantum chemistry computing. It updates a
sequence of subspaces, but now by operating with a preconditioned matrix.
If one can only use preconditioned iterations to solve
linear systems with the underlying matrix,
this is the way to get interior eigenvalues or a cluster of eigenvalues.





Next: Summary of Choices.
Up: Introduction
Previous: Introduction
Contents
Index
Susan Blackford
2000-11-20
![]() matrix can be
stored conveniently, are solved by
direct methods, sometimes also called
transformation methods, where similarity transformations
are applied until the eigenvalues can be easily
read out.
matrix can be
stored conveniently, are solved by
direct methods, sometimes also called
transformation methods, where similarity transformations
are applied until the eigenvalues can be easily
read out.![]() We give a short
review of some current direct methods in §4.2.
We give a short
review of some current direct methods in §4.2.