




Next: Reducing Subspaces.
Up: Singular Case
Previous: Singular Case
Contents
Index
Eigenvalues and Eigenvectors.
The singular case of 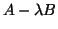 corresponds to either
corresponds to either
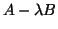 is square and singular for all values of
is square and singular for all values of  , or
, or
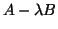 is rectangular.
is rectangular.
Both cases arise in practice, and are significantly more challenging than
the regular case. We outline the theory here and leave details to
§8.7.
Consider
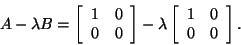 |
(4) |
Then
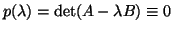 for all
for all  , so
, so
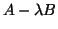 is singular. For any
is singular. For any  ,
,
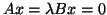 for
for ![$x = [0,1]^T$](img594.png) . But rather than calling all
. But rather than calling all  eigenvalues, we
only call
eigenvalues, we
only call 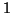 an eigenvalue of this pencil, because
an eigenvalue of this pencil, because
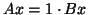 for
for
![$x = [1,0]^T$](img597.png) , and the rank of
, and the rank of 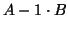 is 0, which is lower than
the rank of
is 0, which is lower than
the rank of 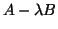 for any other value of
for any other value of  . In general,
if
. In general,
if 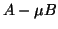 has a lower rank than the rank of
has a lower rank than the rank of 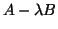 for
almost all other values of
for
almost all other values of  , then
, then 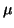 is an eigenvalue.
is an eigenvalue.
Eigenvalues are discontinuous functions of the matrix entries when the
pencil is singular, which is one reason we have to be careful about
definitions. This discontinuity is further discussed below.
Eigenvectors are also no longer so simply defined.
For example, consider
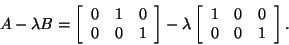 |
(5) |
Then 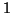 is an eigenvalue but
is an eigenvalue but
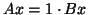 for any
for any ![$x = [z,z,1]^T$](img601.png) for any value of
for any value of 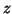 .
Instead we consider reducing subspaces, as defined below.
.
Instead we consider reducing subspaces, as defined below.
 |
(6) |





Next: Reducing Subspaces.
Up: Singular Case
Previous: Singular Case
Contents
Index
Susan Blackford
2000-11-20
![]() corresponds to either
corresponds to either