Inexact Matrix Transformations

The analysis is given for the Cayley transform only, though shift-and-invert could be used as well. The reasons are threefold. First, the shift-and-invert Arnoldi method and the Cayley transform Arnoldi method produce the same Ritz vectors. Second, it makes a link with the (Jacobi) Davidson methods easier to establish. Third, the Cayley transform leads to a more natural approach to the problem.

In the Arnoldi method applied to the Cayley transform, $T_{\mathrm{C}}$, we must solve a sequence of linear systems

$$(A - \mu B) w_j = (A - \nu B) v_j - s_j$$

for $j=1,\ldots,k$, where $s_j$ is the residual and $v_j$ the last Krylov basis vector. The result $w_j$ is orthonormalized against $v_1,\ldots,v_j$ into $v_{j+1}$. One could also apply the Cayley transform to another vector in the Krylov space rather than to $v_j$. In this case, we solve the linear system

$$(A - \mu B) w_j = (A - \nu B) y_j - s_j,$$ (273)

where $y_j$ is chosen as follows: it may be a Ritz vector (Jacobi-Davidson) or the last basis vector (Arnoldi) or the continuation vector (rational Krylov). The residual norm $\Vert s_j\Vert$ is a measure of the backward error since we can rewrite (11.2) as

$$(A - \mu B + s_j w_j^{\ast} / \Vert w_j\Vert^2 ) w_j = (A - \nu B) y_j \ .$$

When a direct method is used, it typically happens that $s_j/ \Vert A-\mu B\Vert \Vert w_j\Vert$ is a modest multiple of machine precision. We say that the direct method computes a backward stable solution of the linear system. Since $\Vert s_j\Vert$ is very small, we talk about an exact eigenvalue solver. Obtaining a small residual norm by an iterative method is also possible but is usually very expensive. In this section, we study the situation where $\Vert s_j\Vert$ is large. In order to give an indication of what we mean by large, a few words about iterative linear system solvers are needed. A linear system $Cx=b$ is said to be solved with a relative residual tolerance $\tau$ when the solution, $x$, satisfies $\Vert b-Cx\Vert \leq \tau\Vert b\Vert.$ Krylov methods [388] are typically used. GMRES [389], BiCGSTAB($\ell$) [410], and QMR [179] are among those most widely used. See [41] for templates for all these solvers. Their performance substantially improves when a suitable preconditioner is employed. Hence what we mean by a large error is that $10^{-8} \leq \tau \leq 10^{-2}.$

By putting all the $s_j$ for $j=1, \ldots,k-1$ together in $S_{k-1}=[s_{1},\ldots,s_{k-1}]$, $w_j$ in $W_{k-1}$ and $y_j$ in $Y_{k-1}$, we obtain

$$(A - \mu B)W_{k-1} = (A -\nu B) Y_{k-1} - S_{k-1} \ .$$ (274)

Let $W_{k-1}^{\dagger}$ be the generalized Moore-Penrose inverse of $W_{k-1}$, i.e., $W_{k-1}^{\dagger} W_{k-1} = I$, and define $E_{k-1} = S_{k-1} W_{k-1}^{\dagger}$. We can rewrite the relation as

$$(A - \mu B + E_{k-1}) W_{k-1} = (A - \nu B) Y_{k-1} \ .$$ (275)

This is the relation that we should obtain after ${k-1}$ steps with the ``inexact'' Cayley transform

$$T_{\mathrm{IC}} = (A - \mu B + E_{k-1})^{-1} (A - \nu B)\ .$$

Note that for a fixed $\nu$ and $\mu$, $T_{\mathrm{IC}}$ depends on $k$ and the way each of the linear systems (11.2) are solved. When (11.2) is solved by a preconditioner $M$ or a stationary linear system solver, i.e., $w_j = M^{-1} (A-\nu B) y_j$ for $j=1, \ldots,k-1$, then $E_{k-1} = E \equiv M - (A-\mu B)$ is independent of $k$ and $y_j$ and so is $T_{\mathrm{IC}}$.

Eigenpairs are computed from ${\rm span}\{v_1,v_2,\ldots,v_k\}$. In Arnoldi's method, this happens by the Hessenberg matrix that arises from the orthogonalization of $W_{k-1}$; in the Davidson method, one uses the projection with $A$ and $B$, e.g., $V_k^{\ast} A V_k z = \theta V_k^{\ast} B V_k z$.

${\rm Span}(v_1,\ldots,v_k)$ contains the eigenvectors associated with the well-separated extreme eigenvalues of $T_{\mathrm{IC}}$. This is a perturbed $T_{\mathrm{C}}$, so the relation with $Ax = \lambda Bx$ is partially lost, and accurately computing eigenpairs of $Ax = \lambda Bx$ may be difficult. To see which parameters play a role in this perturbation, from Theorems 4.3 and 4.4 in [323], it can be shown that if $T_{\mathrm{IC}}$ has distinct eigenvalues, then for each eigenpair $(\zeta,x)$ of $T_{\mathrm{C}}$ there is an eigenpair $(\eta,u)$ of $T_{\mathrm{IC}}$ such that

$$\begin{eqnarray*} \vert\zeta - \eta\vert & \leq & \kappa_1 \vert\zeta\vert \Vert... ...x\Vert & \leq & \kappa_2 \vert\zeta\vert \Vert E_{k-1}\Vert \, , \end{eqnarray*}$$

where $\kappa_1,\kappa_2 > 0$. These inequalities show that if $\Vert E_{k-1}\Vert$ and/or $\zeta$ are small, $(\zeta,x)$ and $(\eta,u)$ correspond very well. In this case, $(\zeta,x)$ can be computed via eigenpairs of $T_{\mathrm{IC}}$. Since $\zeta = (\lambda-\mu)^{-1}(\lambda-\nu)$, $\zeta\approx 0$, is reduced to $\lambda \approx \nu$.

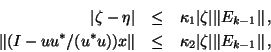
This section can be concluded as follows.

• The inexact Cayley transform behaves like the exact one. This implies that eigenvalues near the pole $\mu$ are still targeted.

• However, the eigenvalues are perturbed. The level of perturbation depends on $E_{k-1}$. For any $E_{k-1}$, the transformation is able to compute eigenvalues near $\nu$ accurately. In practice, this means that only one (simple) eigenvalue can be computed very accurately. It also implies that $\nu$ needs to be updated from time to time, since $\lambda$ is unknown. The other eigenvalues are only computed approximately depending on the error level $\Vert E_{k-1}\Vert$.

• The sequence (11.2) for $j=1, \ldots,k-1$ defines a Krylov subspace $\KK^k(T_{\mathrm{IC}}, y_1)$.

The remaining question is now how to compute the eigenpairs of $T_{\mathrm{IC}}$ or how to exploit them for computing eigenpairs of $Ax = \lambda Bx$. In §11.2.3 and §11.2.4, we discuss the Rayleigh-Ritz technique; i.e., eigenpairs are computed from the orthogonal projection of $Ax = \lambda Bx$ on the ${\rm span}(v_1,\ldots,v_k)$. In §11.2.7, the eigenpairs are computed from the eigenpairs of $T_{\mathrm{IC}}$ directly by use of the rational Krylov recurrence relation. §11.2.6 presents a Lanczos algorithm that uses the recurrence relation for the eigenvectors and the Rayleigh-Ritz projection for the eigenvalues.

Note that $\mu$ and $\nu$ cannot be chosen too far away from each other. Suppose the eigenvalue $\lambda$ is wanted. From the conclusion given above, the convergence is faster when $\mu$ is chosen close to $\lambda$, and the computed eigenvalue can only be accurate when $\nu$ is close to $\lambda$. In theory, one could select $\mu=\nu$, which is usually used in the Davidson method. Since $T_{\mathrm{C}}=I$ in that case, there is a high risk of stagnation in the latter method. A robust selection is used in the Jacobi-Davidson method, which we discuss in §11.2.5.