Direct Solvers for Band Matrices

This section is analogous to §10.3.1 for dense matrices:

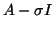$A-\sigma I$ is Hermitian definite.

In this case Cholesky is the algorithm of choice. It is implemented in LAPACK computational routines xPBTRF to compute the factorization and xPBTRS to solve using the factorization (both are combined in LAPACK driver routine xPBSVX). Cholesky is implemented in analogous ScaLAPACK routines PxPBTRF, PxPBTRS, and PxPBSV.

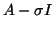$A-\sigma I$ is non-Hermitian.

In this case Gaussian elimination is the algorithm of choice. It is implemented in LAPACK computational routines xGBTRF to compute the factorization and xGBTRS to solve using the factorization (both are combined in LAPACK driver routine xGBSVX). It is implemented in analogous ScaLAPACK routines PxGBTRF, PxGBTRS, and PxGBSV with partial pivoting, and PxDBTRF, PxDBTRS, and PxDBSV without pivoting (which is risker but faster than using pivoting).

No routines exploiting Hermitian indefinite structure are available (because there is no simple bound on how much the bandwidth can grow because of pivoting). No band routines are in MATLAB. If 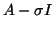$A-\sigma I$ is Hermitian and the bandwidth is narrow enough (such as tridiagonal), direct eigensolver methods from §4.2 should be used.