




Next: Jacobi-Davidson Method G. Sleijpen and
Up: Transformation to Standard Problems
Previous: Split-and-invert .
Contents
Index
Shift-and-Invert.
None of the transformations to standard form, (8.3),
(8.4), or (8.5), can be used when both  and
and  are singular or when
are singular or when  is ill-conditioned.
An attractive and popular technique is to apply first the shift to the
original problem and then carry out the split-invert. This is the
SI, as discussed
in §3.3. Specifically, let
is ill-conditioned.
An attractive and popular technique is to apply first the shift to the
original problem and then carry out the split-invert. This is the
SI, as discussed
in §3.3. Specifically, let 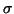 be a user-selected
shift such that the matrix
be a user-selected
shift such that the matrix 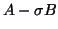 is nonsingular; then the
original problem (8.1) can be transformed to
is nonsingular; then the
original problem (8.1) can be transformed to
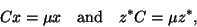 |
(219) |
where
We see that the eigenvalues  of the
problem (8.1) closest to the shift
of the
problem (8.1) closest to the shift 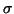 are mapped
as the exterior eigenvalues of the reduced standard eigenvalue
problem (8.6), that is, to the eigenvalues of largest magnitude,
and these are the eigenvalues that are first well approximated by the
iterative methods.
are mapped
as the exterior eigenvalues of the reduced standard eigenvalue
problem (8.6), that is, to the eigenvalues of largest magnitude,
and these are the eigenvalues that are first well approximated by the
iterative methods.
In practice, an effective shift selection depends on the user's
preferences and on knowledge
of the underlying generalized eigenproblem.
A good shift not only amplifies the
desired eigenvalues, but it also leads to a well-conditioned
matrix 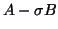 . This often makes the task of selecting good shifts
a challenging one.
. This often makes the task of selecting good shifts
a challenging one.
For the application of an iterative method for the reduced standard
eigenvalue problem (8.6), one needs to evaluate
matrix-vector products
or
for given vectors 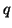 and
and 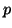 .
For an efficient evaluation, let
.
For an efficient evaluation, let
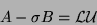 |
(220) |
represent some convenient factorization of 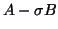 , where
, where 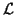 and
and
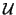 are square matrices. Since
are square matrices. Since 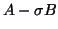 is assumed
to be nonsingular, the factors
is assumed
to be nonsingular, the factors 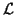 and
and 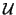 are
also nonsingular. The factorization should be chosen so that
the corresponding
linear systems of equations with
are
also nonsingular. The factorization should be chosen so that
the corresponding
linear systems of equations with 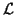 ,
,
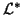 and/or
and/or 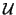 ,
,
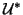 can be solved
efficiently, and typically, sparse LU factorizations are used.
See §10.3.
Of course, one can also select
can be solved
efficiently, and typically, sparse LU factorizations are used.
See §10.3.
Of course, one can also select
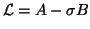 and
and
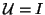 if this leads to convenient linear systems.
if this leads to convenient linear systems.
With the above factorization, the matrix-vector product
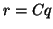 can be evaluated as follows:
can be evaluated as follows:
(a) form 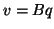 ,
,
(b) solve 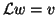 for
for 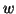 ,
,
(c) solve 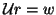 for
for 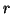 .
.
Similar, the matrix-vector product
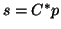 can be evaluated as
following three steps:
can be evaluated as
following three steps:
(a)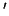 solve
solve 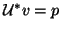 for
for 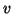 ,
,
(b) solve
solve 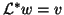 for
for 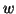 ,
,
(c) form
form 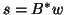 .
.
The SI technique is a powerful tool
in the treatment of the generalized eigenvalue
problem (8.1). The major problem, which often becomes bottleneck,
is to find a convenient factorization (8.7) of
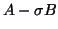 so that the associated linear systems of equations
can be solved efficiently. If accurate solution of the linear systems with
so that the associated linear systems of equations
can be solved efficiently. If accurate solution of the linear systems with
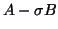 becomes too expensive, then one may consider the usage of
inexact Cayley transformations (see §11.2), or the
Jacobi-Davidson method.
becomes too expensive, then one may consider the usage of
inexact Cayley transformations (see §11.2), or the
Jacobi-Davidson method.





Next: Jacobi-Davidson Method G. Sleijpen and
Up: Transformation to Standard Problems
Previous: Split-and-invert .
Contents
Index
Susan Blackford
2000-11-20
![]() . This often makes the task of selecting good shifts
a challenging one.
. This often makes the task of selecting good shifts
a challenging one.
![]() can be evaluated as follows:
can be evaluated as follows:
,
for
,
for
.
solve
for
,
solve
for
,
form
.
![]() so that the associated linear systems of equations
can be solved efficiently. If accurate solution of the linear systems with
so that the associated linear systems of equations
can be solved efficiently. If accurate solution of the linear systems with
![]() becomes too expensive, then one may consider the usage of
inexact Cayley transformations (see §11.2), or the
Jacobi-Davidson method.
becomes too expensive, then one may consider the usage of
inexact Cayley transformations (see §11.2), or the
Jacobi-Davidson method.