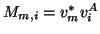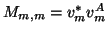Next: Schur Form and Restart
Up: Jacobi-Davidson Methods G. Sleijpen
Previous: Jacobi-Davidson Methods G. Sleijpen
Contents
Index
Generalization of Hermitian Case
Similar to the Lanczos methods and the Arnoldi method, the
Jacobi-Davidson method constructs a subspace onto which the given
eigenproblem is projected. The subspace is constructed with approximate
shift-and-invert steps, instead of forming a Krylov subspace. In
§4.7 we have explained the method in detail, and the
generalization to the non-Hermitian case for the basic algorithm,
described in Algorithm 4.13 (p. ![[*]](http://www.netlib.org/utk/icons/crossref.png) ),
is quite straightforward. In fact, the changes are:
),
is quite straightforward. In fact, the changes are:
- The construction of the matrix
 has to take into account that
has to take into account that  is non-Hermitian, hence the corresponding action in (7)-(9) has to be
replaced by
is non-Hermitian, hence the corresponding action in (7)-(9) has to be
replaced by
for 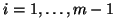
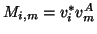 ,
, 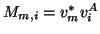
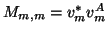
- In (10) a routine has to be selected for the non-Hermitian dense matrix
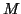
If the correction equation (in step (15) of the algorithm) is
solved exactly, then the approximate eigenvalues have quadratic
convergence towards the eigenvalues of  .
.
Susan Blackford
2000-11-20
![]() ),
is quite straightforward. In fact, the changes are:
),
is quite straightforward. In fact, the changes are:
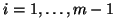
,