




Next: Remarks on Clustered Eigenvalues.
Up: Some Combination of and
Previous: Error Bound for Computed
Contents
Index
Error Bound for Computed Eigenvectors.
Keep the assignments to
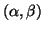 , let
, let
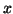 be the eigenvector of
be the eigenvector of 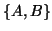 corresponding to
corresponding to
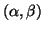 ,
and let
,
and let 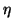 be the smallest distance in chordal metric between
be the smallest distance in chordal metric between
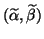 and all the other eigenvalues
of the pair. Then we have
and all the other eigenvalues
of the pair. Then we have
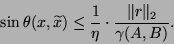 |
(107) |
This bound also needs information on
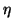 , besides the residual error
, besides the residual error 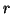 and
and 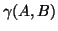 .
Usually such information
is available after a successful computation by,
e.g., the shift-and-invert Lanczos
algorithm which usually delivers eigenvalues in the neighborhood
of a shift and consequently yields good information on the
.
Usually such information
is available after a successful computation by,
e.g., the shift-and-invert Lanczos
algorithm which usually delivers eigenvalues in the neighborhood
of a shift and consequently yields good information on the
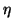 .
.
Susan Blackford
2000-11-20