




Next: Error Bound for Computed
Up: Some Combination of and
Previous: Residual Vector.
Contents
Index
Transfer Residual Error to Backward Error.
It can be proved that there are Hermitian matrices 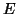 and
and 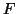 , e.g.,
, e.g.,
![\begin{displaymath}
(E,F) = \left[-r\wtd x^*-\wtd x r^*
+\left(\wtd\beta\wtd x^...
...\wtd x^*\right]\cdot
\left(\wtd\beta I, -\wtd\alpha I\right),
\end{displaymath}](img1668.png) |
(104) |
such that
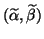 and
and 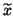 are an exact eigenvalue and
its corresponding eigenvector of
are an exact eigenvalue and
its corresponding eigenvector of 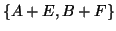 .
We are interested in such matrices
.
We are interested in such matrices 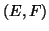 with smallest possible norms.
It turns out that the best possible
with smallest possible norms.
It turns out that the best possible
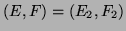 for the
spectral norm
for the
spectral norm 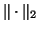 and the best possible
and the best possible
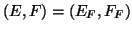 for Frobenius norm
for Frobenius norm 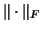 satisfy
satisfy
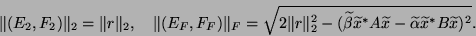 |
(105) |
See [256,431,473].![[*]](http://www.netlib.org/utk/icons/footnote.png) In fact,
In fact, 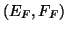 is given explicitly by (5.40).
Therefore if
is given explicitly by (5.40).
Therefore if 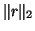 is small,
the computed
is small,
the computed
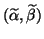 and
and 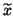 are exact ones
of nearby matrices. Error analysis of
this kind is called backward error analysis and
matrices
are exact ones
of nearby matrices. Error analysis of
this kind is called backward error analysis and
matrices 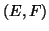 are backward errors.
are backward errors.
We say an algorithm
that delivers an approximate eigenpair
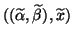 is
is
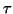 -backward stable for the pair with respect to the norm
-backward stable for the pair with respect to the norm
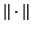 if it is an exact eigenpair for
if it is an exact eigenpair for 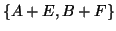 with
with
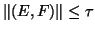 .
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
.
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
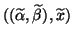 .
In convention, an algorithm is called backward stable
if
.
In convention, an algorithm is called backward stable
if
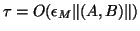 .
.





Next: Error Bound for Computed
Up: Some Combination of and
Previous: Residual Vector.
Contents
Index
Susan Blackford
2000-11-20
![]() is
is
![]() -backward stable for the pair with respect to the norm
-backward stable for the pair with respect to the norm
![]() if it is an exact eigenpair for
if it is an exact eigenpair for ![]() with
with
![]() .
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
.
With these in mind,
statements can be made about the backward stability of the algorithm which
computes the eigenpair
![]() .
In convention, an algorithm is called backward stable
if
.
In convention, an algorithm is called backward stable
if
![]() .
.