




Next: Convergence Properties
Up: Implicitly Restarted Lanczos Method
Previous: Shift Selection
Contents
Index
Lanczos Method in GEMV Form
At each restart in Algorithm 4.7 we have a
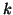 -step Lanczos factorization
-step Lanczos factorization
or, for 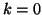 a starting vector
a starting vector 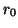 .
Algorithm 4.8 gives a template for applying
.
Algorithm 4.8 gives a template for applying 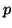 additional
Lanczos steps
to extend this to an
additional
Lanczos steps
to extend this to an 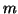 -step Lanczos factorization
-step Lanczos factorization
We will now describe some implementation details, referring to the
respective phases in Algorithm 4.8.
- (2)
- If started from scratch (
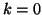 ) take
) take 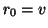 as a starting
vector.
Ideally, for eigenvalue
calculations, one should attempt to construct a
as a starting
vector.
Ideally, for eigenvalue
calculations, one should attempt to construct a 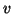 that is dominant
in eigenvector directions of interest. In the absence of any other
considerations, a random vector is a reasonable choice.
that is dominant
in eigenvector directions of interest. In the absence of any other
considerations, a random vector is a reasonable choice.
- (3)
- Normalize
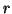 to get the new basis vector
to get the new basis vector 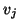 .
The norm
.
The norm
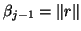 has already been computed at step (7) for the previous
has already been computed at step (7) for the previous 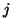 .
.
- (5)
- This is the Lanczos three-term recurrence step to orthogonalize
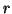 with
respect to the two most recent columns of
with
respect to the two most recent columns of 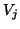 . It is organized in modified
Gram-Schmidt form.
. It is organized in modified
Gram-Schmidt form.
- (7)
- The sequence of statements in this if clause assure that the
new residual direction
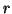 is numerically orthogonal to the previously
computed directions, i.e., to all of the columns of
is numerically orthogonal to the previously
computed directions, i.e., to all of the columns of 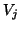 .
The parameter
.
The parameter 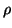 must be specified (
must be specified (
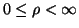 ).
The test asks the question, ``Is
).
The test asks the question, ``Is 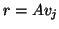 nearly in
the space that already has been constructed?"
The ratio
nearly in
the space that already has been constructed?"
The ratio
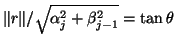 ,
where
,
where 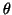 is the angle that the vector
is the angle that the vector 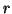 makes with the
range space of
makes with the
range space of 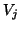 .
A larger value of
.
A larger value of 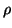 is a more stringent orthogonality requirement.
With
is a more stringent orthogonality requirement.
With 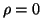 , the algorithm reverts to the standard Lanczos process
without reorthogonalization. One step of this correction may not
be sufficient and it should be implemented as an iteration
with the test for subsequent corrections being
, the algorithm reverts to the standard Lanczos process
without reorthogonalization. One step of this correction may not
be sufficient and it should be implemented as an iteration
with the test for subsequent corrections being
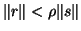 ;
see the discussion in [96].
If a suitable
;
see the discussion in [96].
If a suitable 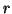 has not been generated after a fixed number of attempts
(say five), then
has not been generated after a fixed number of attempts
(say five), then 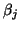 should be set to zero and a randomly generated
vector should be orthogonalized against the basis
should be set to zero and a randomly generated
vector should be orthogonalized against the basis 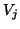 and put in place
of
and put in place
of 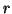 to continue the factorization.
We suggest setting
to continue the factorization.
We suggest setting 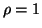 .
.
It is well known that the classical three-term Lanczos scheme will
fail to produce orthogonal vectors precisely when a Ritz value
(approximate eigenvalue) converges to an eigenvalue of  .
To remedy this, we have included an iterative
refinement technique which maintains orthogonality to full working
precision at a very reasonable cost. The special situation imposed by
implicit restart makes this modification essential for obtaining
accurate eigenvalues and numerically orthogonal eigenvectors. The
implicit restart mechanism will be less effective and may even fail
if numerical orthogonality is not maintained.
.
To remedy this, we have included an iterative
refinement technique which maintains orthogonality to full working
precision at a very reasonable cost. The special situation imposed by
implicit restart makes this modification essential for obtaining
accurate eigenvalues and numerically orthogonal eigenvectors. The
implicit restart mechanism will be less effective and may even fail
if numerical orthogonality is not maintained.





Next: Convergence Properties
Up: Implicitly Restarted Lanczos Method
Previous: Shift Selection
Contents
Index
Susan Blackford
2000-11-20
![]() .
To remedy this, we have included an iterative
refinement technique which maintains orthogonality to full working
precision at a very reasonable cost. The special situation imposed by
implicit restart makes this modification essential for obtaining
accurate eigenvalues and numerically orthogonal eigenvectors. The
implicit restart mechanism will be less effective and may even fail
if numerical orthogonality is not maintained.
.
To remedy this, we have included an iterative
refinement technique which maintains orthogonality to full working
precision at a very reasonable cost. The special situation imposed by
implicit restart makes this modification essential for obtaining
accurate eigenvalues and numerically orthogonal eigenvectors. The
implicit restart mechanism will be less effective and may even fail
if numerical orthogonality is not maintained.