




Next: Selective Reorthogonalization.
Up: Reorthogonalization
Previous: Reorthogonalization
Contents
Index
We could play it safe and do a full reorthogonalization either by
modified or classical Gram-Schmidt, in the latter case computing the
orthogonalization coefficients in a vector
and then subtracting
to get the improved vector 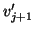 . If the norm is decreased by a
nontrivial amount, say
. If the norm is decreased by a
nontrivial amount, say
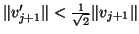 ,
this will have to be repeated, but this will hardly ever happen when
treating properly computed Lanczos vectors.
,
this will have to be repeated, but this will hardly ever happen when
treating properly computed Lanczos vectors.
Susan Blackford
2000-11-20