




Next: Multiple Eigenvalues.
Up: Lanczos Method A.
Previous: Algorithm
Contents
Index
Convergence Properties
There is a beautiful theory, based on the properties of orthogonal
polynomials, that describes when eigenvalues converge. The
characteristic polynomials of the tridiagonal matrices 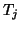 are
orthogonal polynomials with respect to a scalar product, defined by
the expansion of the starting vector
are
orthogonal polynomials with respect to a scalar product, defined by
the expansion of the starting vector 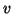 as a sum of eigenvectors.
One gets bounds on differences
as a sum of eigenvectors.
One gets bounds on differences
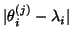 between
the eigenvalues
between
the eigenvalues
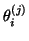 of
of 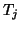 and
and 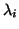 of
of  by replacing these
unknown orthogonal polynomials with the well-known Chebyshev
polynomials, the so-called Kaniel-Paige-Saad bounds; see
[353].
by replacing these
unknown orthogonal polynomials with the well-known Chebyshev
polynomials, the so-called Kaniel-Paige-Saad bounds; see
[353].
This theory says that we get convergence to those eigenvalues that are
represented in the starting vector and faster convergence to those in
the ends of the spectrum. The better separated these are from the rest
of the eigenvalues, the faster will they converge.
In practical cases, we are often interested just in the lowest
eigenvalues, and fortuitously these are among the first to
converge. On the other hand, the relative separation of the lowest
eigenvalues is often poor, since the separation is relative to
the whole spread of the spectrum, not to the distance to the origin.
Subsections





Next: Multiple Eigenvalues.
Up: Lanczos Method A.
Previous: Algorithm
Contents
Index
Susan Blackford
2000-11-20