Accuracy and Refinement of the DLAM




Next: The LU factorization
Up: The Distributed Linear
Previous: The BLACS Network
When applying numerically the results obtained by the DLAM, we choose
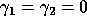 , assuming that the cost of these instructions
will always be negligible compared to BLACS operations or a Level 3
instruction. We determined
, assuming that the cost of these instructions
will always be negligible compared to BLACS operations or a Level 3
instruction. We determined 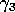 as being the achieved peak
performance of the BLAS matrix-multiply GEMM. This approximation
is incorrect for small block sizes, in which case Level 2 operations
are performed and
as being the achieved peak
performance of the BLAS matrix-multiply GEMM. This approximation
is incorrect for small block sizes, in which case Level 2 operations
are performed and 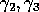 should be set respectively to
the achieved peak performance of the BLAS matrix-vector multiply GEMV
and zero. Obviously, these coarse approximations could be refined by
computing a piece-wise linear approximation of the
should be set respectively to
the achieved peak performance of the BLAS matrix-vector multiply GEMV
and zero. Obviously, these coarse approximations could be refined by
computing a piece-wise linear approximation of the 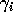 's with
respect to the problem size. This model smoothes the influence of the
physical memory hierarchy and could be adapted to out-of-core BLAS
operations.
's with
respect to the problem size. This model smoothes the influence of the
physical memory hierarchy and could be adapted to out-of-core BLAS
operations.
Modeling the performance of the DLAM network is tightly coupled to
the physical network. Experimental values of 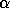 and
and  can easily be determined for a given machine. If the logical mesh
can be embedded into the physical network and the message collisions
ignored,
can easily be determined for a given machine. If the logical mesh
can be embedded into the physical network and the message collisions
ignored, 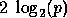 is a good approximation of
is a good approximation of
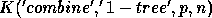 assuming the result has to be left on
the
assuming the result has to be left on
the 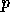 processes and neglecting the cost of the local computations;
similarly,
processes and neglecting the cost of the local computations;
similarly, 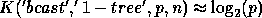 . When the
communications can be pipelined, it is reasonable to estimate
. When the
communications can be pipelined, it is reasonable to estimate
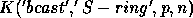 by 2.
Because this model ignores the probable collision of messages or
possible network contention problems, its accuracy depends on the
number of physical links. For instance, when comparing the performance
obtained on an ideal DLAM with those obtained on an ethernet based
network of workstations sharing one physical link, it is important
to use appropriate values for
by 2.
Because this model ignores the probable collision of messages or
possible network contention problems, its accuracy depends on the
number of physical links. For instance, when comparing the performance
obtained on an ideal DLAM with those obtained on an ethernet based
network of workstations sharing one physical link, it is important
to use appropriate values for  . Indeed, an upper bound for
. Indeed, an upper bound for
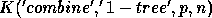 is given by
is given by  . However, for
a given value of
. However, for
a given value of 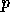 , it is possible to experimentally determine
constants which take into account the cost due to network contention
and message collisions. More accurate models taking into account the
collisions of messages could be used, but this is beyond the scope
of this paper. Finally, the described model could obviously be
refined by computing a piece-wise linear approximation of the time
for sending a message with respect to the message length.
, it is possible to experimentally determine
constants which take into account the cost due to network contention
and message collisions. More accurate models taking into account the
collisions of messages could be used, but this is beyond the scope
of this paper. Finally, the described model could obviously be
refined by computing a piece-wise linear approximation of the time
for sending a message with respect to the message length.




Next: The LU factorization
Up: The Distributed Linear
Previous: The BLACS Network
Antoine Petitet
Fri Mar 31 13:01:26 EST 1995
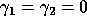 , assuming that the cost of these instructions
will always be negligible compared to BLACS operations or a Level 3
instruction. We determined
, assuming that the cost of these instructions
will always be negligible compared to BLACS operations or a Level 3
instruction. We determined 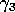 as being the achieved peak
performance of the BLAS matrix-multiply GEMM. This approximation
is incorrect for small block sizes, in which case Level 2 operations
are performed and
as being the achieved peak
performance of the BLAS matrix-multiply GEMM. This approximation
is incorrect for small block sizes, in which case Level 2 operations
are performed and 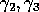 should be set respectively to
the achieved peak performance of the BLAS matrix-vector multiply GEMV
and zero. Obviously, these coarse approximations could be refined by
computing a piece-wise linear approximation of the
should be set respectively to
the achieved peak performance of the BLAS matrix-vector multiply GEMV
and zero. Obviously, these coarse approximations could be refined by
computing a piece-wise linear approximation of the 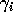 's with
respect to the problem size. This model smoothes the influence of the
physical memory hierarchy and could be adapted to out-of-core BLAS
operations.
's with
respect to the problem size. This model smoothes the influence of the
physical memory hierarchy and could be adapted to out-of-core BLAS
operations.
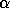 and
and  can easily be determined for a given machine. If the logical mesh
can be embedded into the physical network and the message collisions
ignored,
can easily be determined for a given machine. If the logical mesh
can be embedded into the physical network and the message collisions
ignored, 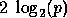 is a good approximation of
is a good approximation of
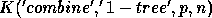 assuming the result has to be left on
the
assuming the result has to be left on
the 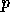 processes and neglecting the cost of the local computations;
similarly,
processes and neglecting the cost of the local computations;
similarly, 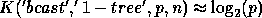 . When the
communications can be pipelined, it is reasonable to estimate
. When the
communications can be pipelined, it is reasonable to estimate
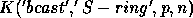 by 2.
Because this model ignores the probable collision of messages or
possible network contention problems, its accuracy depends on the
number of physical links. For instance, when comparing the performance
obtained on an ideal DLAM with those obtained on an ethernet based
network of workstations sharing one physical link, it is important
to use appropriate values for
by 2.
Because this model ignores the probable collision of messages or
possible network contention problems, its accuracy depends on the
number of physical links. For instance, when comparing the performance
obtained on an ideal DLAM with those obtained on an ethernet based
network of workstations sharing one physical link, it is important
to use appropriate values for  . Indeed, an upper bound for
. Indeed, an upper bound for
 . However, for
a given value of
. However, for
a given value of