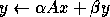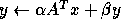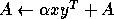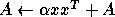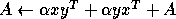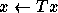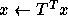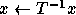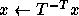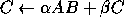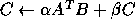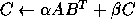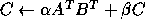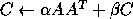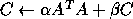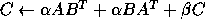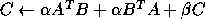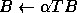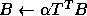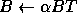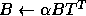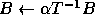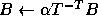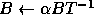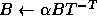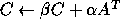-
{
}*

-
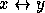

-
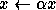

-
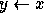

-
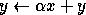

-
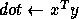

-
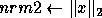

-
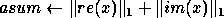

- Index and value of the first maximal element in absolute value of a vector.
- Matrix-vector products
-
- Rank-1 update of a general matrix
-
- Rank-1 and rank-2 updates of a symmetric matrix
-
- Multiplication by a triangular matrix
-
- Solving a triangular system of equations
-
- Matrix-matrix products
-
- Rank-
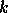 and rank-
and rank-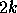 updates of a symmetric matrix
updates of a symmetric matrix
-
- Multiplication by a triangular matrix
-
- Solving multiple triangular systems of equations
-
- Matrix transposition
-
Here 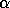 and
and 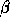 are scalars,
are scalars,  and
and 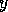 are
vectors,
are
vectors, 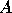 ,
, 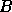 and
and 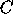 are rectangular matrices
(in some cases square and symmetric), and
are rectangular matrices
(in some cases square and symmetric), and 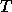 is an
upper or lower triangular matrix (and nonsingular
for the triangular solves).
is an
upper or lower triangular matrix (and nonsingular
for the triangular solves).
Analogous operations are proposed in complex arithmetic. Conjugate transposition is specified as well as simple transposition. Additional operations are provided for scaling a complex vector by a real scalar and updates of a Hermitian matrix as follows:
-
{
}*

-
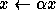

-
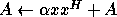

-
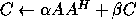

-
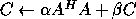
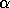 and
and 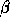 real for the vector-vector and
matrix-matrix operations, and
real for the vector-vector and
matrix-matrix operations, and
-
{
}*

-
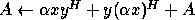

-
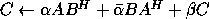

-
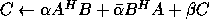
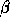 real.
real.