Figure 1: Linda Environment
Linda [9] is a concurrent programming model that has evolved from a Yale University research project. The primary concept in Linda is that of a ``tuple-space'', an abstraction via which cooperating processes communicate. This central theme of Linda has been proposed as an alternative paradigm to the two traditional methods of parallel processing, viz. that based on shared memory, and on message passing. The tuple-space concept is essentially an abstraction of distributed shared memory, with one important difference (tuple-spaces are associative), and several minor distinctions (destructive and non-destructive reads, and different coherency semantics are possible). Applications use the Linda model by embedding explicitly, within cooperating sequential programs, constructs that manipulate (insert/retrieve tuples) the tuple space.
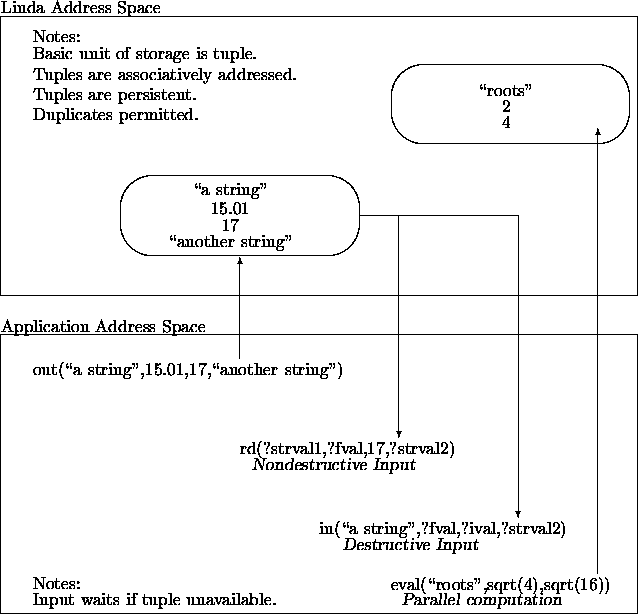
From the application point of view Linda [4] is a set of programming language extensions for facilitating parallel programming. The Linda model is a scheme built upon an associative memory referred to as tuple-space It provides a shared memory abstraction for process communication without requiring the underlying hardware to physically share memory. The model is illustrated in Figure 2 [9].
Tuples are collections of fields logically ``welded'' to form persistent storage items. They are the basic tuple-space storage units. Parallel processes exchange data by generating, reading, and consuming them. To update a tuple, the tuple is removed from tuple-space, modified, and returned to tuple-space. Restricting tuple-space modification in this manner creates an implicit locking mechanism ensuring proper synchronization of multiple accesses.
The following are the four basic operations or primitives which are added to a language to produce a Linda dialect. Figure 2 depicts the operational environment when using Linda.
Tuples are selected by the rd() or in() primitives on the basis of their field values. There are no tuple addresses in an associative memory. Consider the following tuple:
A variety of access routes to this tuple are possible, e.g., any one of the following operations suffices:
The ``?'' operator designates a value returned from a matching tuple. Fields marked by the operator do not participate in the (associative memory) matching process. Any of the three example rd() operations results in a non-destructive reading of the original tuple. If the operation were an in(), the tuple would be removed from tuple-space.
To illustrate the eval() primitive, consider the following:
eval("roots",sqrt(4),sqrt(16))
Using Linda terminology, this creates a live tuple. The square-root operations are performed independent of the originating process, with the (two) numeric results combined to form a three element tuple saved in tuple-space. The eval() primitive is a mechanism capable of creating fine grain parallelism.
The ``Linda System'' usually refers to a specific (sometimes portable) implementation of software that supports the Linda programming model. System software is provided that establishes and maintains tuple spaces, that is used in conjunction with libraries that appropriately interpret and execute Linda primitives. Depending on the environment (shared memory multiprocessors, message passing parallel computers, networks of workstations etc), the tuple space mechanism is implemented using different techniques, and with varying degrees of efficiency. Recently, a new system technique has been proposed, at least nominally related to the Linda project. This scheme, termed ``Pirhana'' proposes a proactive approach to concurrent computing - the idea being that computational resources (viewed as active agents) seize computational tasks from a well known location based on availability and suitability. Again, this scheme may be implemented on multiple platforms, and manifested as a ``Pirhana system'' or ``Linda-Pirhana system''.