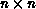For the selected program segment, the programmer picks one of the choices (1) through (3), and specifies the data partitioning via an interface provided by the tool. The tool responds by creating an internal data mapping that specifies the mapping of the data to a set of virtual processors. The number of virtual processors is equal to the number of partitions indicated by the data partitioning. The mapping of the virtual processors onto the physical processors is assumed to be done by the run time system, and this mapping is unspecified in the software layer. Henceforth, we will use the term ``processor'' synonymously with ``virtual processor.'' The internal data mapping is used by the performance estimator to compute an estimate of communication and other costs for the program segment. It is also used by the tool to determine the data that needs to be communicated between the processors.
Let us continue with our example program segment, and see how the
internal mapping is constructed for partitioning (2), that is, A
partitioned by column and B by row. The data mappings for the other
two cases can be constructed in a similar manner. Let A and B be of size
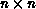and the number of (virtual) processors be p. For simplicity we
assume that p divides n. The following two data mappings are
computed:\
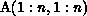partitioned by column: Create a virtual array
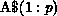, where 
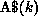represents the kth column partition
of A, that is, A$ consists of the elements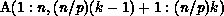 
.
The virtual array is only an internal entity, used within the tool to
maintain the mapping of data to (virtual) processors. It does not have any
physical storage on the machine. The partition of A represented by
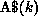is assumed to be mapped onto the kth processor by default.
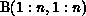partitioned by row: Create a virtual array
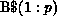, where 
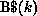represents the ith row partition of
B, that is, B$ consists of the elements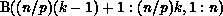 
.
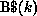is assigned to the kth processor by default.
The internal data mapping is used to solve the following two problems:\
.
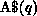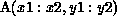, what processors contain
elements of this section? This is given by the set of processors
.
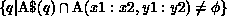A useful technique that we will subsequently use on these sections is
called ``translation.'' Translation refers to the conversion of an accessed
section computed with respect to a particular loop to the section accessed
with respect to an enclosing loop. For example, consider a reference
to a two-dimensional array within a doubly nested loop. The section
of the array accessed within each iteration of the innermost loop
is a single element. The same reference, when evaluated with respect to the
entire inner loop (i.e., all iterations of the inner loop) may access a
larger section, such as a column of the array. If we evaluated the reference
with respect to the outer loop (i.e., all iterations of the outer loop), we
may notice that the reference results in an access of the entire array in a
columnwise manner. Translation is thus a method of converting array sections
in terms of enclosing loops, and we will denote this operation
by the symbol ``
''.
The tool uses (1) to determine which processors should do what computations. The general rule used is: each processor executes only those program statements whose l-values are in its local storage. The l-values computed by a processor are said to be owned by the processor. In order to compute an l-value, several r-values may be required, and not all of them may be local to that processor. The inverse mapping (2) is used to determine the set of processors that own the desired r-values. These processors must send the r-value they own to the processor that will execute the statement.
The data mapping scheme described above works only for arrays. Scalar variables are assumed to be replicated, that is, every processor stores a copy of the scalar variable in its local memory. By the rule stated earlier, this implies that any statement that computes the value of a scalar is executed by all the processors.